The acceleration time graph of the motion of a particle from A to B is semicircle with radius of √7 . Find the velocity of particle at t2 at it t1 velocity is 3m/sec[π=22/7] .
![The acceleration time graph of the motion of a particle from A to B is semicircle with radius of sqrt(7) . Find the velocity of particle at t(2) at it t(1) velocity is 3m//sec [pi = 22//7] .](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_P03_17_MPST_P1_XI_E01_023_Q01.png)
152m/sec
8m/sec
172m/sec
None of these
The correct Answer is:C
The acceleration …………..
we known that change in velocity = Area under a - t curve.
∴Vt2−Vt1 = Area under the graph and t - axis from D to B (which is quaether circle)
∴Vt2−Vt1=πr24=227×(√7)24=
∴Vt2−3=112or=112+3=172m/sec
Similar Questions
The acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionAcceleration - time graph of a particle moving in a straight line is shown in figure. Velocity of particle at time t = 0 is 2ms−1. Find velocity at the end of fourth second.

View Solution
Knowledge Check
The acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
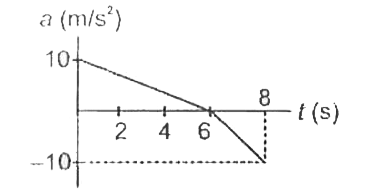 A+15m/sB+20m/sC−15m/sD−20m/s
A+15m/sB+20m/sC−15m/sD−20m/sThe acceleration time graph of a particle is shown in the figure-1.140. What is the velocity of particle at t=8s, if initial velocity of particle is 3 m/s? (Assume motion is 1 dimension) :
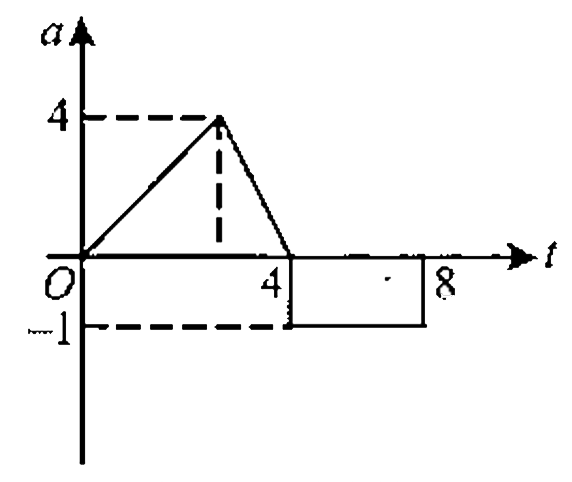 A4 m/sB5 m/sC6 m/sD7 m/s
A4 m/sB5 m/sC6 m/sD7 m/sThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.A41m/sB4m/sC39m/sD27m/s
Starting from rest, acceleration of a particle is a=2t(t−1). The velocity of the particle at t=5s is
View SolutionThe acceleration of a particle which starts from rest varies with time according to relation a=2t+3. The velocity of the particle at time t would be
View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
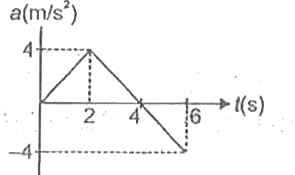
View SolutionThe acceleration of a particle, moving in a straight line, at time t is (2t+1)m/sec2 . If 4m/sec is the initial velocity of the particle then its velocity after 2 sec. is
View Solution
