Two equal masses each in are hung from a balance whose scale pans differ in vertical height by $h$ . The error in weighing in terms of density of the earth $ρ$ is

Video Solution

Text Solution

Verified by Experts

$g_{h} = [1 - \frac{2 h}{R_{e}}], W_{2}, W_{1} = m g_{2} - m g_{1} = 2 m g [\frac{h_{1}}{R_{e}} - \frac{h_{2}}{R_{e}}] = 2 m \frac{G M}{R_{e}^{2}} \times \frac{h}{R_{e}} [∵ g = \frac{G M}{R_{e}^{2}} & h_{1} - h_{2} = h]$
Error in weighing $= W_{2} - W_{1} = 2 m G \frac{4}{3} π R_{e}^{3} ρ \frac{h}{R_{e}^{3}} = \frac{8 π}{3} G m ρ h$
Due to depth
Assuming density of earth remains same throughout
At earth surface, $g = \frac{4}{3} π G R_{e} ρ$ ...(i) at depth d inside the earth
For point P only mass of the inner sphere is effective $g_{d} = \frac{G M'}{r^{2}}$
$g_{d} = \frac{G}{r^{2}} \times \frac{M r^{2}}{R_{e}^{2}} = \frac{G M}{R_{e}^{2}} \times \frac{r}{R_{e}} = \frac{G M}{R_{e}^{2}} \times \frac{R_{e} - d}{R_{e}}$
Mass of sphere of radius $r = M'$
$M' = \frac{4}{3} π r^{3} ρ = \frac{4}{3} π r^{3} \times \frac{M}{4 / 3 π R^{3}} = M' = \frac{M}{R^{3}} r^{3}$
$g_{d} = g [1 - \frac{d}{R_{e}}]$ valid for any depth.

Updated on:21/07/2023

Two equal masses each $m$ are hung from a balance whose scale pans differ in vertical height by $h$ . The error in weighing is
A $π G ρ m h$
B $\frac{1}{3} G ρ m h$
C $\frac{8}{3} π G ρ m h$
D $\frac{4}{3} π G ρ m h$
Two equal masses each in are hung from a balance whose scale pans differ in vertical height by $h$ . The error in weighing in terms of density of the earth $ρ$ is
A $π G ρ m h$
B $\frac{1}{3} π G ρ m h$
C $\frac{8}{3} π G ρ m h$
D $\frac{4}{3} π G ρ m h$
Two identical blocks of mass m are suspended from a beam balance whose scale pans differ in vertical height by $h (< < R)$ , if R and $ρ$ are the radius and density of the earth, then the error in weighing is

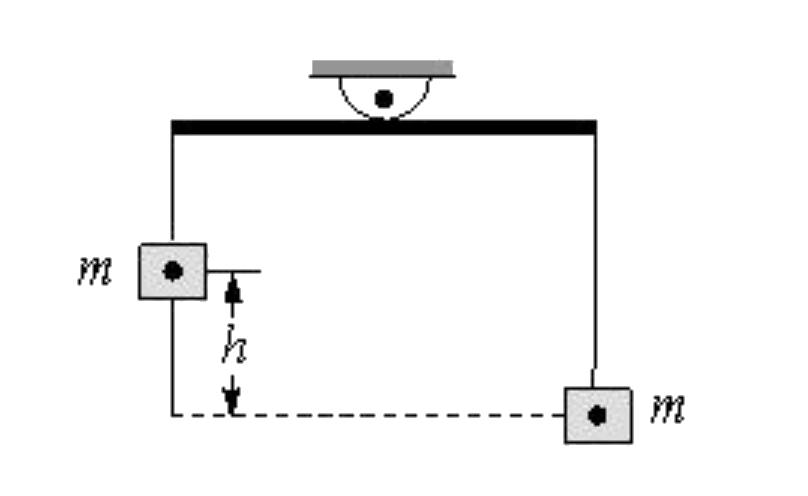A $\frac{2}{3} π ρ R^{3} G m$
B $\frac{8}{3} π ρ G m h$
C $\frac{8}{3} π ρ R^{3} G m$
D $\frac{4}{3} π ρ G m^{2} h$