A cylindrical vessel filled with water up to a height of 2m stands on a horizontal plane. The side of the vessel has a plugged circular hole so that the vessel begins to move on the floor it the plug is removed. The coefficient of friction between the bottom of the vessel and the plane is 0.4, and total mass of water plus vessel is 100kg.
From torricelli's theorem, velocity of efflux =(2gh)
Momentum per second carried by water stream (efflux)
= density ×volume coming out per second × velocity =ρ×av×v=ρav2
Hence force on cylinderical cessel =ρa2gh
Cylinder starts to move when reaction force is just equal to maximum force of friction i.e.,
μMg=ρa2gh⇒a=μM2ρh=0.4×1002×103×2=0.01m2
Area of circular hole =πd24=0.01m2⇒d=√0.01×4π=0.113m
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)
16 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A cylindrical vessel filled with water upto a height of 2m stands on horizontal plane. The side wall of the vessel has a pugged circular hole touching the bottom. If the minimum diameter of the hole so that the vessel begins to move on the floor if the plug is removed is x10√π meter then x will be (if the coefficient of frication between the bottom of the vessel and the plane is 0.4 and total mass of water plus vessel is 100kg.)
View SolutionA cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
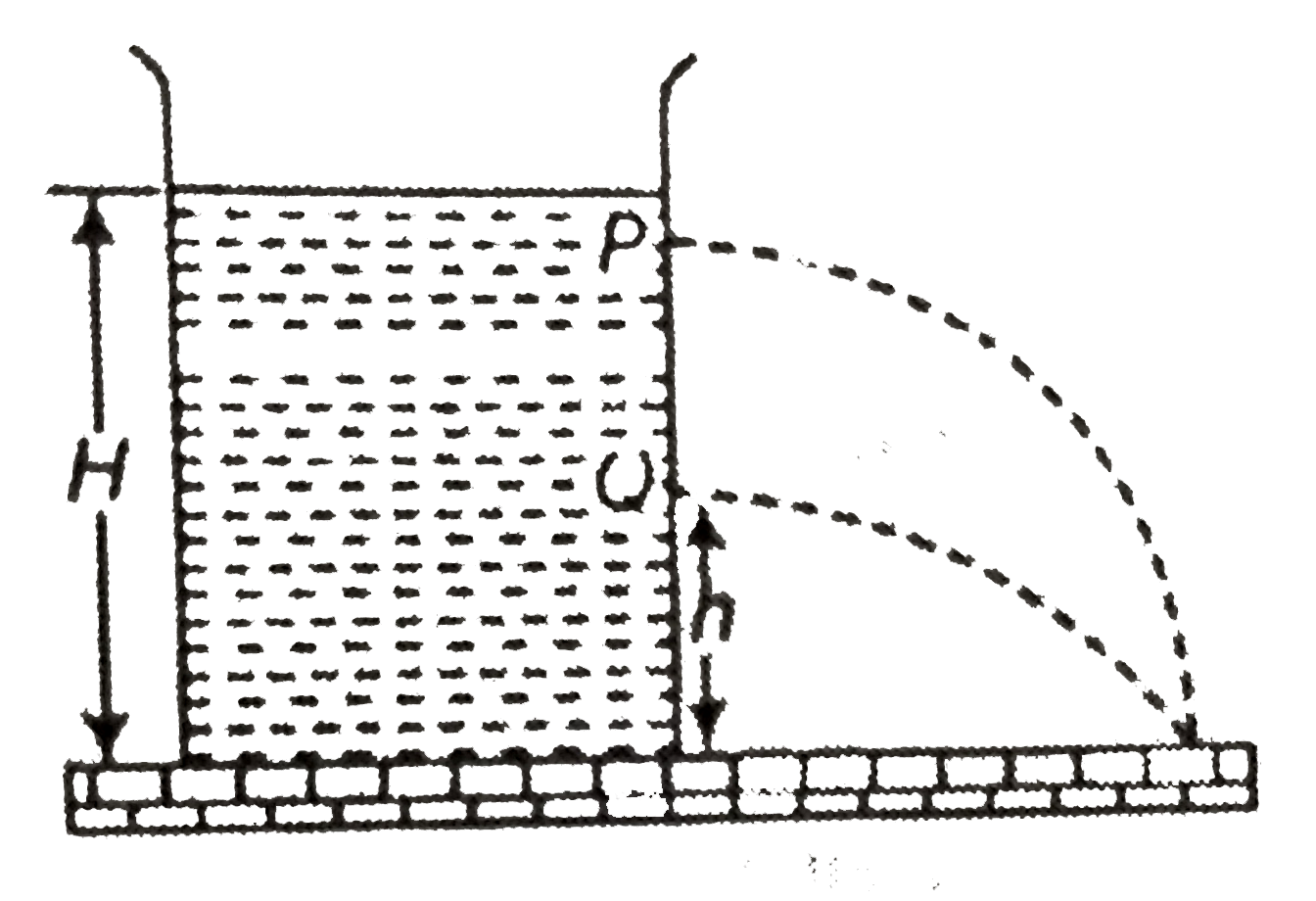
View Solution
Knowledge Check
A cylindrical vessel filled with water upto a height of 2m stands on horizontal plane. The side wall of the vessel has a pugged circular hole touching the bottom. If the minimum diameter of the hole so that the vessel begins to move on the floor if the plug is removed is x10√π meter then x will be (if the coefficient of frication between the bottom of the vessel and the plane is 0.4 and total mass of water plus vessel is 100kg.)
A√2μMπρHB√μM2πρHC√μMρHDnoneA cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
AH/4BH/2C3H/4DHA cylindrical vessel of radius R and height H and open at the top is completely filled with y . A small circular hole of radius r is made near the bottom of vessel . The time taken for 25 % of water to flow out is
A√2Hg(√3−1)BR2r2√2Hg(1+2√3)CR2r2√2Hg(1−2√3)DR2r2√2Hg(√3−1)
A wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionWater level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.

View SolutionA cylindrical vessel of radius 3 cm has at the bottom a horizontal capallary tube of length 20 cm and intrnal radius 0.4 mm. If the vessel is filled with water, find the time taken by it to empty one half of its contents. Given that the viscosity of water is 0.01 poise.
View SolutionTwo cylindrical vessels of equal cross-sectional area. A contain water upto height h1 and h2. The vessels are interconnected so that the levels in them becomes equal. The work done by the force of gravity during the process is:
View Solution
