A conducting rod MN moves with a speed v parallel to a long straight wire which carries a constant current i, as shown in fig. The length of the rod is normal to the wire. Find the emf induced in the total length of the rod. State which end will be at a lower potential.
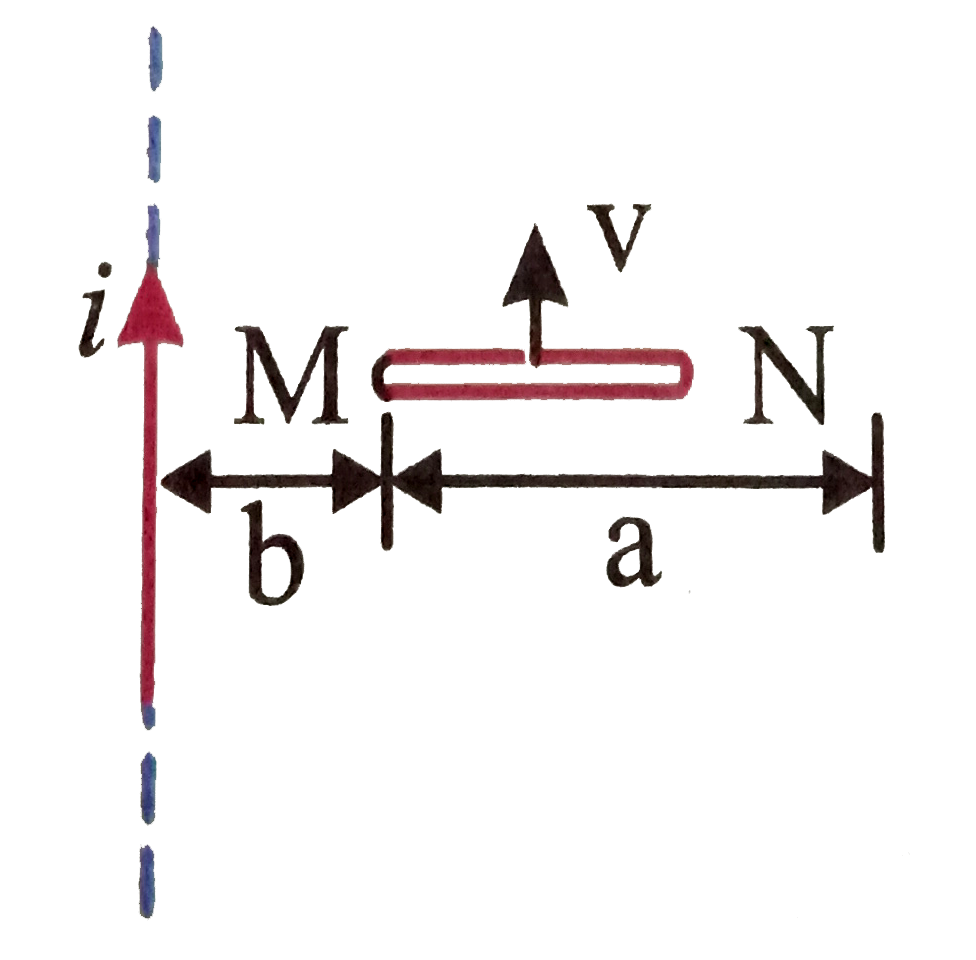
The magnetic field induction due to current i is different at different sections of the rod, because they are at different distances from the wire.
Let us, first of all, subdivide the entire length of the conductor MN into elementry sections. Consider a section (shown shaded in the figure (b)) of thickness dx at a distance x from the wire. As all the three, v,B and (dX) are mutually normally to each other, so the emf induced in it is de=Bvdx. ( from N to M by Fleming's right hand rule )

For the sections, the induced emf is in the same sence, (i.e., from N to M)
∴ Total emf induced in the conductor is
e=∫de=∫b+abBvdx
Substituting for B=μ0i2πx, the above equations gets changes to e=∫b+abμ0ivdx2πxe=μ0iv2π[lnx]b+ab or, e=μ0iv2πln(1+a/b)
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:C.U.Q 1
Explore 51 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Assertion & Reason
Explore 11 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -4
Explore 43 Videos
- ELECTRO MAGNETIC WAVESBook:NARAYNAChapter:ELECTRO MAGNETIC WAVESExercise:LEVEL-II(H.W)
Explore 14 Videos
Similar Questions
A copper rod of length L is moving at a uniform speed v parallel to along straight wire carrying a current of I as shown in figure-5.25. The rod is perpendicular to the wire with its ends at distance a and b from if . Calculate the motional EMF induced in the rod.
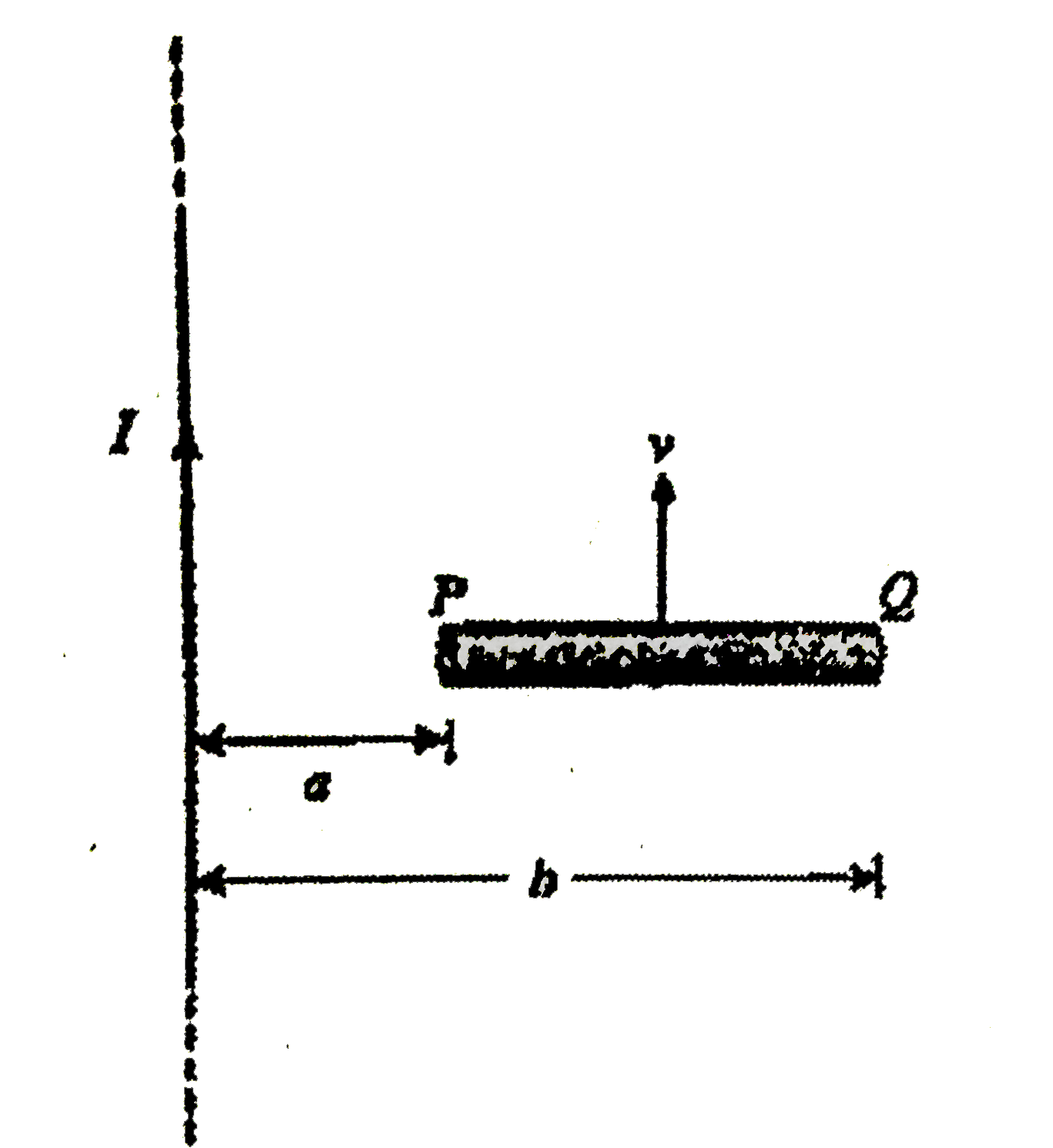
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View Solution
Knowledge Check
A copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
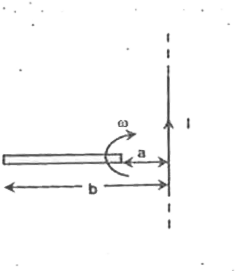 Aμ0i(wa)2πIn(ba)Bμ0i(wb)2πIn(ba)CzeroDμ0iw(a+b)4πIn(ba)
Aμ0i(wa)2πIn(ba)Bμ0i(wb)2πIn(ba)CzeroDμ0iw(a+b)4πIn(ba)A cionducing rod moves with constant velocity v perpendicular to the straight wire carrying a current I as shown compute that the emf generated between the ends of the rod
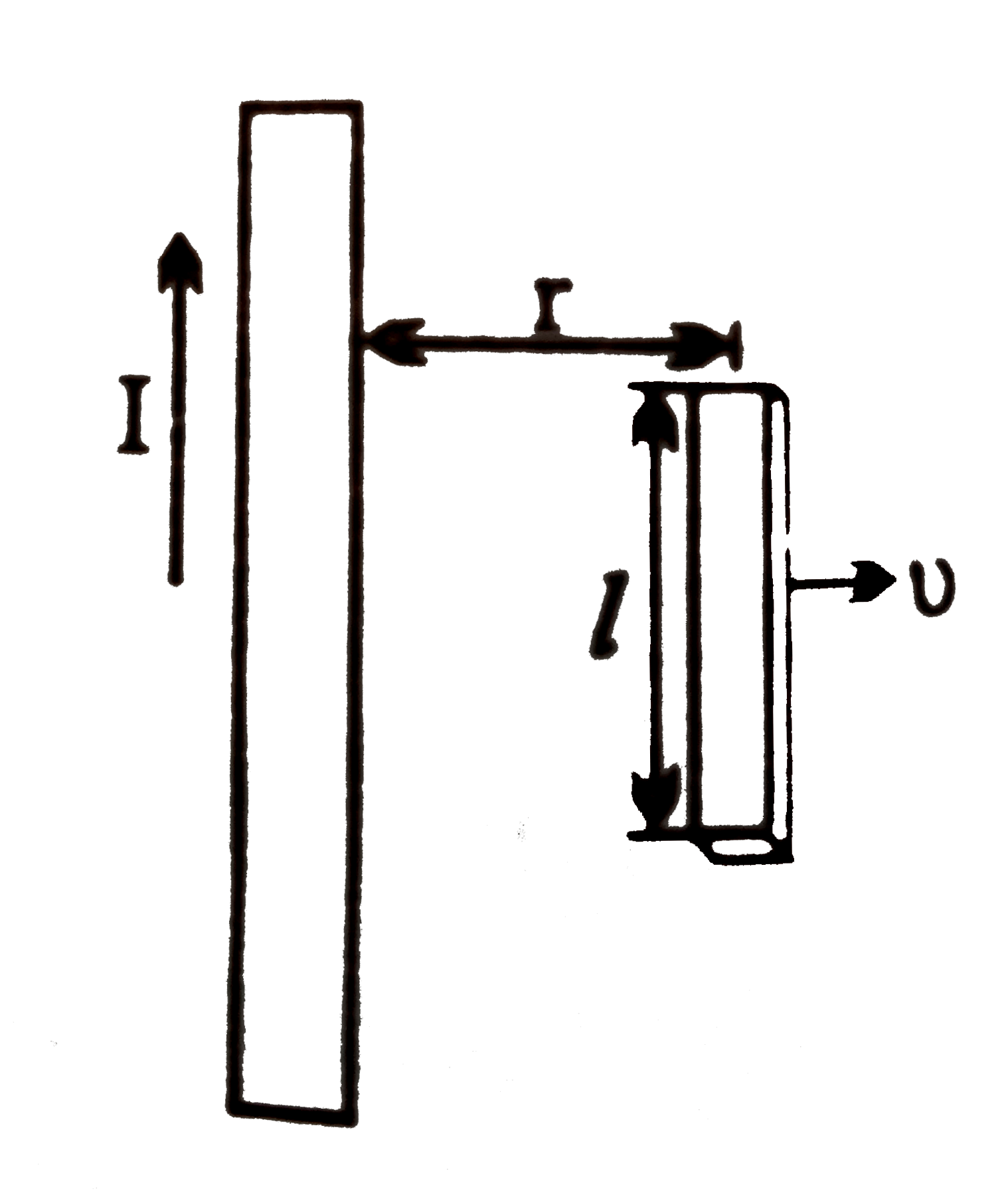 Aμ0vIlπrBμ0vIl2πrC2μ0vIlπrDμ0vIl4πr
Aμ0vIlπrBμ0vIl2πrC2μ0vIlπrDμ0vIl4πr
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.AAt θ=37∘ velocity of end A is 43v0 downwardsBAt θ=37∘ angular velocity of rod is 5v03lCAngular velocity of rod is constantDvelocity of end A is constant.
A rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v.F∈dtheemf∈duced∈thewirewhenitsdistance∈thewirewhenitsdistanceomthelongwireisx.
View SolutionA conducting rod length 1m moves with a speed of 2m/s parallel to a straight long wire carrying 4A current. Axis of rod is kept perpendicular to the wire with its near end at a distance of 1m from the wire. Magnitude of induced emf in rod is N×10−7log16volt. Find the value of N.
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance ‘a’ from the wire.
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
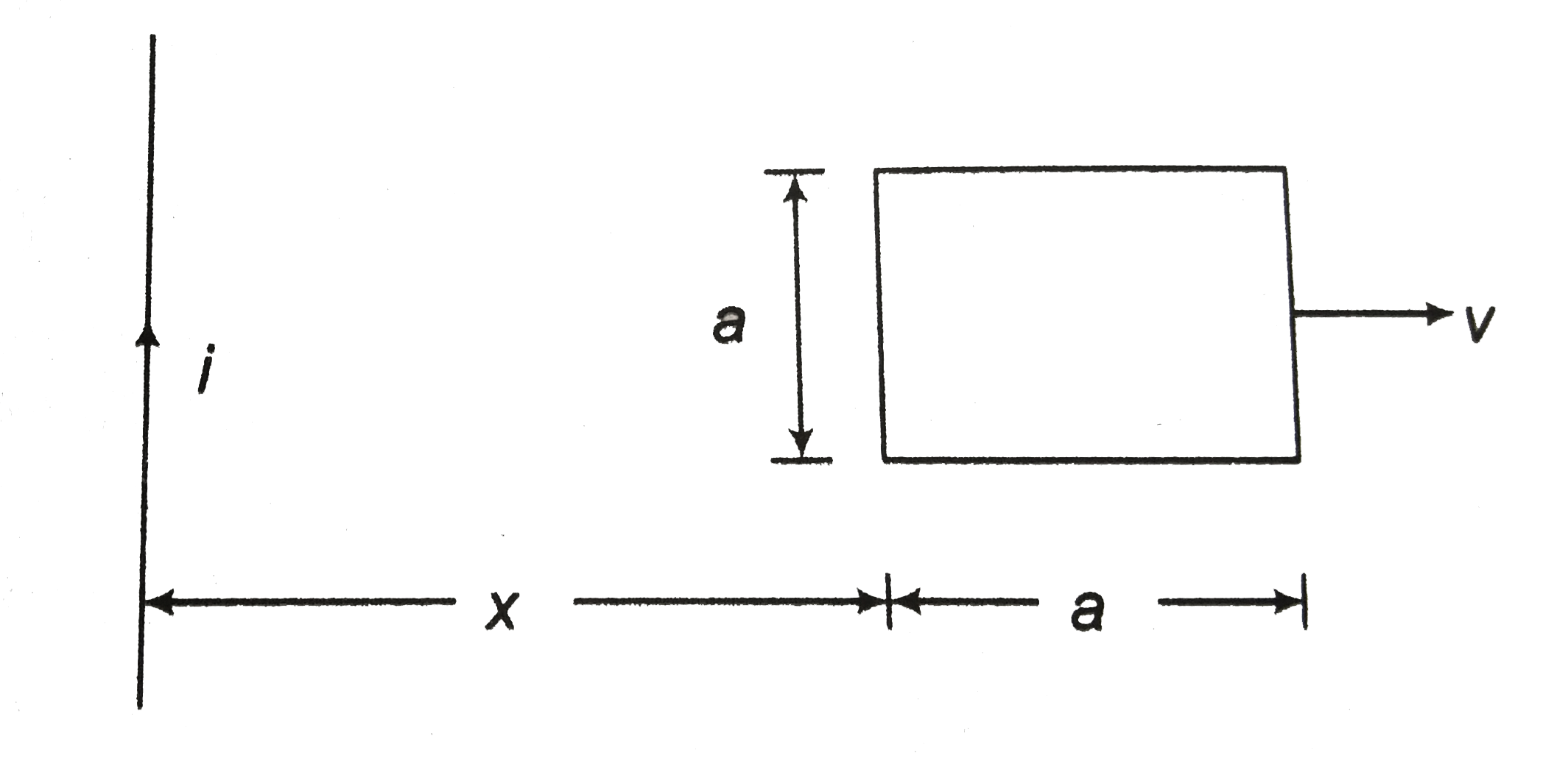
View SolutionThree long, straight parallel wires carrying current, are arranged as shown in figure. The force experienced by a 25cm length of wire C is

View Solution

