Two capacitor of capacitance $5 μ F$ and $10 μ F$ are charged to potential $40 V$ and $10 V$ respectively. Now the two capacitors ate connected with plates of same polarities together .
(A) the common potential will be $20 V$
(B) the final charges of capacitors will be $100 μ C$ and $200 μ C$
(c) the ratio of total energy stored in capacitors before and after connection is $3 : 2$
(D) the loss energy of system is $1500 μ J$

$A, B, C$

$B, C, D$

$A, B, D$

$A, B, C, D$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Two capacitors of capacitances $1 μ F and 3 μ F$ are charged to the same voltages 5V. They are connected in parallel with oppositely charged plates connected together. Then
AFinal common voltage will be 5V
BFinal common voltage will be 2.5
CHeat produced in the circuit will be zero
DHeat produced in the circuit will be $37.5 μ J$
Two capacitors of $2 μ F$ and $3 μ F$ are charged to $150 V$ and $120 V$ , respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity $1.5 μ F$ falls to the free end of the wire. Then

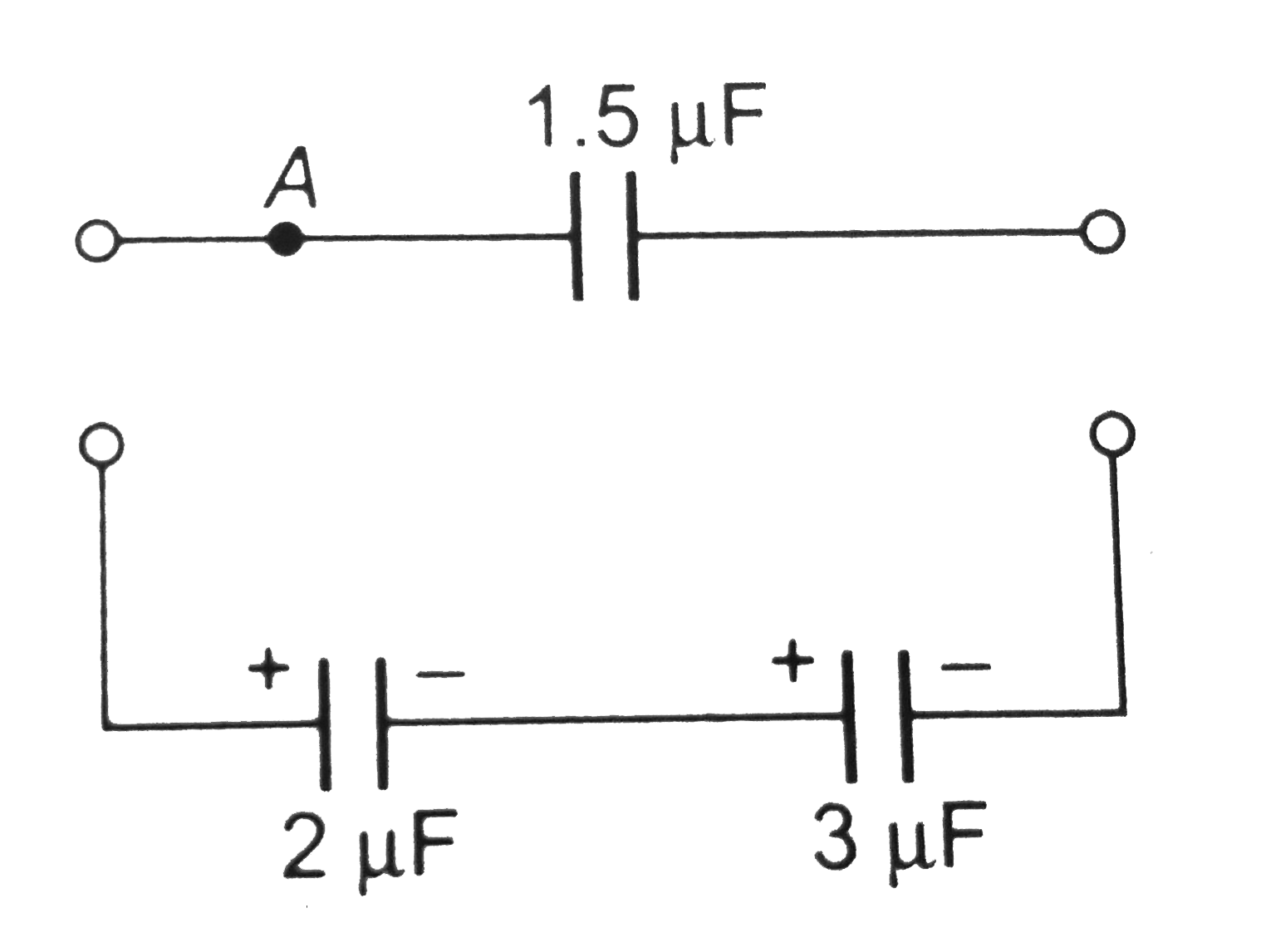Achargeg on $1.5 μ F$ capacitor is $180 μ F$
Bcharge on $2 μ F$ capacitor is $120 μ F$
Cpositive chasrge flows through A from right to left
Dpositive charge flows through A from left to right
Two capacitors of capacitances $3 μ F$ and $6 μ F$ are charged to a potential of $12 V$ each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each will be
A $6$ volt
B $4$ volt
C $3$ volt
DZero