A particle is moving in a straight line so that after 't' seconds its distance is 'S' (in cms) from a fixed point of the line is given be S=f(t)=8t+t3.
Find (i) the velocity at time t=2 (ii) the initial velocity (iii) acceleration at t=2 secSolution in Telugu
The correct Answer is:20 cm/sec, 8 cm/sec, 12 cm/sec2
Step by step video, text & image solution for A particle is moving in a straight line so that after 't' seconds its distance is 'S' (in cms) from a fixed point of the line is given be S=f(t)=8t+t^3. Find (i) the velocity at time t=2 (ii) the initial velocity (iii) acceleration at t=2 sec by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:SRISIRI PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:10.4 MEAN VALUE THEOREMS - VSAQ
Explore 8 Videos
- APPLICATIONS OF DERIVATIVESBook:SRISIRI PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:10.5 MAXIMA AND MINIMA - LAQ
Explore 8 Videos
- APPLICATIONS OF DERIVATIVESBook:SRISIRI PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:10.2 TANGENT AND NORMAL - LAQ
Explore 8 Videos
- ADDITION OF VECTORSBook:SRISIRI PUBLICATIONChapter:ADDITION OF VECTORSExercise:SPQ
Explore 7 Videos
- BOARD MODEL PAPER-1Book:SRISIRI PUBLICATIONChapter:BOARD MODEL PAPER-1Exercise:QUESTIONS
Explore 24 Videos
Similar Questions
Verify Rolle's theorem for the function y=f(x)=x2+4on [-3,3]
View SolutionFind the maximum area of the rectangle that can be formed with fixed perimeter 20.
View SolutionShow that the tangent at P(x1,y1) on the curve √x+√y=√a is xx−121+yy−121=a12
View SolutionLet ¯a=¯i+2¯j+3¯kand¯b=3¯i+¯j. . Find a unit vector in the direction of ¯a+¯b
View SolutionIf A={0,π6,π4,π3,π2}andf:A→B is a surjection defined by f(x)=cosx then find B.
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f . If the sum of the distances travelled in t^(th) and (t + 1)^(th) seconds is 100 cm , then its velocity after t seconds, in cm//s , is.
View Solutionएक कण एक सीधी रेखा में गतिमान है। सेकण्ड बाद रेखा में दिये गये बिन्दु से इसकी दूरी मीटर में s=t33−t22−6t+5 द्वारा प्रदत्त है। तब ज्ञात कीजिए-
(i) 5 सेकण्ड बाद कण का वेग क्या होगा? था
(ii) जब कण का वेग शून्य है तब इसका त्वरण क्या होगा?
View Solutionसरल रेखा में गतिमान एक कण का त्वरण (a) समय (t) ग्राफ संलग्न चित्र में प्रदर्शित है। कण का प्रारम्भिक वेग 2 मीटर/सेकण्ड है। ज्ञात कीजिए (i) t=3 सेकण्ड तथा t=6 सेकण्ड पर कण का वेग (ii) t=0 से t=6 सेकण्ड के बीच कण का औसत त्वरण।
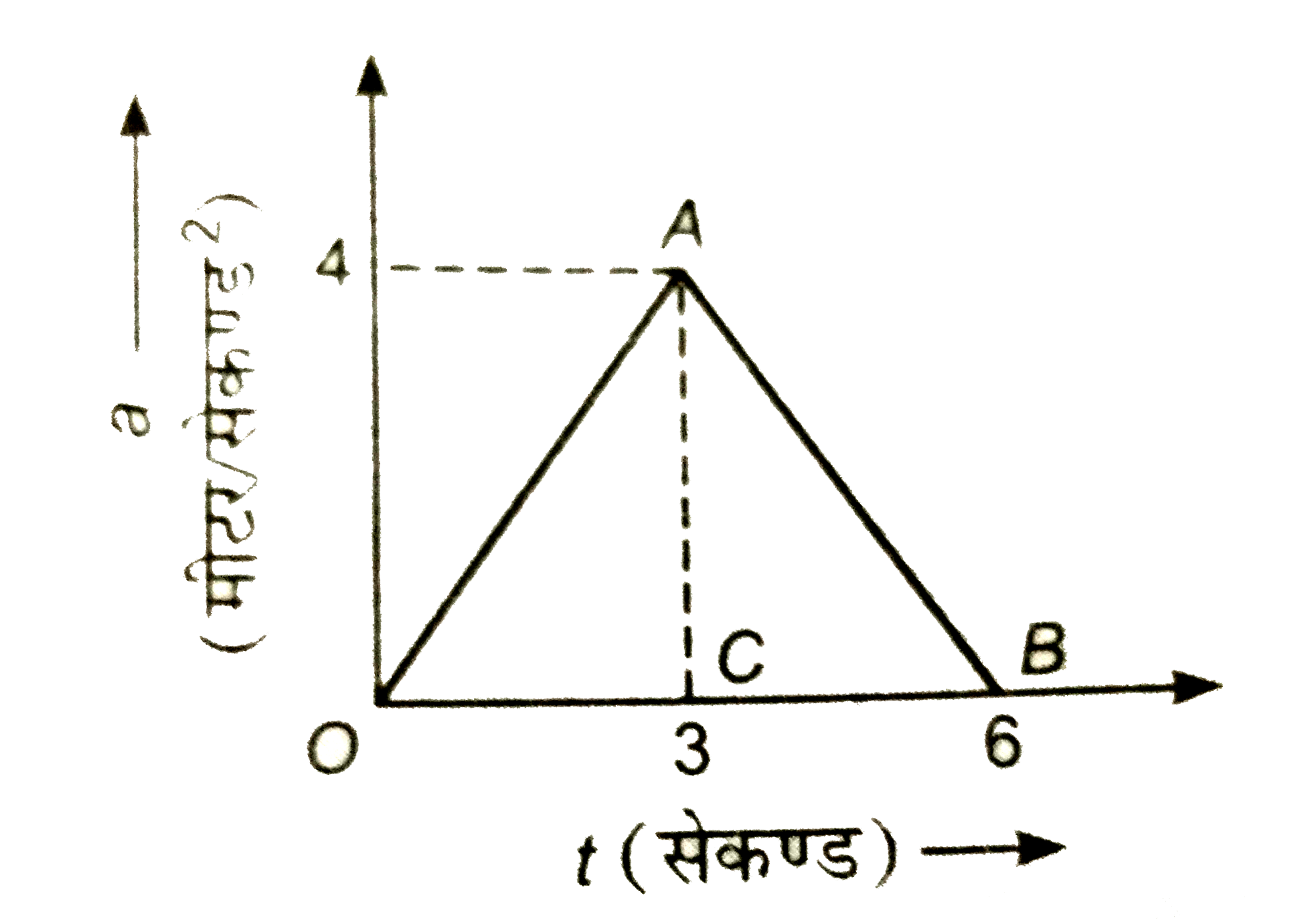
View SolutionThe acceleration of a particle moving along a straight line is (6t2−3t)cm/s2, at time t seconds. If the velocity of the particel at time 2 seconds be 10cm/s, find its velocity at time t seconds.
View Solutionएक कण एक सरल रेखा में इस तरह से चलता हैं ताकि इसका स्थिति t सेकेण्ड के बाद s(t)=6t−t2 हैं | इसका प्रारंभिक वेग क्या हैं।
View SolutionA particle is moving in a straight line so that after 't' seconds its distance is 'S' (in cms) from a fixed point of the line is given be S=f(t)=8t+t3.
Find (i) the velocity at time t=2 (ii) the initial velocity (iii) acceleration at t=2 sec
View SolutionA particle is moving in a straight line and its distance x cm from a fixed point on the line at any time t seconds is given by ,
x=112t4−23t3+32t2+t+15.
At what time is the velocity minimum ? Also find the minimum velocity.
View SolutionA particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec
View SolutionA particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f . If the sum of the distances travelled in t^(th) and (t + 1)^(th) seconds is 100 cm , then its velocity after t seconds, in cm//s , is.
View SolutionA particle moves in a straight line such that its distance in 't' seconds from a fixed point is (6t−t2) cm. find its velocity at the end of t=2 sec.
View Solution

