Question

Cone

Explanation

Cone

This chapter revolves around the concept of cone, including shapes of cone, the surface area of cone and volume of the cone. Students would be able to get the right understanding of how to solve different problems as we have included solved problems at the end.

What is a Cone?

A cone is a shape which is formed by the lines that connect a common point. This is known as the vertex or apex. When it comes to the height of the cone, it is the distance from the vertex of the cone to the base. It is important to know that the slant height is the length of the cone from apex to any point and that too on the circumference of the base. So, there are lots of different formulas which are derived for the volume and surface area of the cone bases on these quantities. You can look at the figure below where the cone is defined by the radius of the base, its height and slant height.

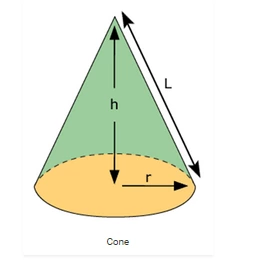
Cone Formula

It is on the basis of the radius (r), height (h) and slant height (/) that the formula for the surface area as well as the volume of the cone is derived.  So, we will try to explain this in the easiest manner.

Slant Height

The distance from the apex or vertex to the point on the outer line of the circular base of the cone is the slant height of the cone. Coming to the formula for the slant height, it can be derived by the Pythagoras Theorem. So,

Slant Height, l = √(r²+h²)

Volume of the Cone

It is possible to write the volume of the cone (V) having a radius as r and height h from the vertex to the base and / is the length of the edge of the cone. So, the volume of the cone is:

Volume(V) = ⅓ πr²h

Surface Area of the Cone

The sum of its lateral surface area(πrl) as well as the surface area of the circular base(πr²) is the surface area of a right circular cone. So, we can write the total surface of the cone as πr/ + πr²

Or Area = πr(l + r)

The value of slant height can be put and where the area of the cone can also be calculated.

Types of Cone

Now, we will study the types of cones. Well, cones are of two types – Right Circular Cone and Oblique Cone. Let us have a good look at these types of cones.

• 
  

  Right Circular Cone:  A cone has a circular base, and the axis from the vertex of the cone towards the base passes through the center of the circular base is termed as the Right Circular Cone. It is just above the center of the circular base that vertex of the cone lies.  It is because of the axis that forms a right angle with the base of the cone or is perpendicular to the base that the word right is used here. In geometry, this is the most used common cones. You can look at the figure below, which is an example of a right circular cone.

  
  


• 
  

  Oblique Cone: A cone which has a circular base but the axis of the cone is not perpendicular with the base, is known as Oblique cone. The location of the vertex of this cone is directly above the centre of the circular base. For this reason this cone looks like a tilted cone or slanted cone.

  
  

Properties of Cone

Now, we will have a look at the properties of the cone, which are as follows:

• A cone has no edge but only one face, which is the circular base.


• There is only one vertex or apex point.


• The total surface of the cone is πr( l +r ).


• The volume of the cone is ½ πr²h.


• The slant height of the cone is √(r²+h²)

Related Videos:

• Cone: slant height: volume:CSA: TSA


• Frustum of a cone: formation and formulas ( slant height: volume: CSA: TSA)


• Hemisphere: volume: CSA: TSA


• Cylinder: volume: CSA: TSA


• Sphere: volume: SA


• Pyramid: volume: SA

Now, to understand the types of questions that are asked in the examination, we will have a look at some of the solved problems.

Question 1: The radius of a cone has a base of 21 cm and a height of 28 cm. Can you calculate the volume of the cone?

Solution: Here, we find that

r = 21 cm and h = 28 cm

Now the volume of cone = 1/3 π r² h

V = 1/3 (3.14 x 21 x 21 x 28)

V = 1/3 x 38772.72

Therefore, the volume of a cone = 12924.24 cm³

Question 2:  The height of a cone is 15 cm, and its volume is 770 cm³. Can you find the radius of its base?

Solution:  Given,

 h = 15 cm and V = 770 cu.cm

Now, the volume of cone = 1/3 π r² h

so, 770 = 1/3 x 3.14 x r 2 x 15

now, 770 = 3.14 x r 2 x 5

⇒ 770 = 15.7 x r²

⇒ r² = 770 / 15.7 = 49

⇒ 2 = 49

Therefore r = 7 cm.

Question 3:  ABC is a right triangle with sides of measure 5 cm, 12 cm and 13 cm, which is revolved about the side 12 cm. Can you find the volume of the solid so obtained?

Solution: We can find that the triangle revolved about the side 12 cm.

Here, radius = r = 5m and height = h = 12 cm

Now, Volume = 1/ 3 π r² h

So, V = 1/3 x 3.14 x 5 x 5 x 12

Therefore, V = 314 cm³

Question 4:  The radius of the cone r = 4 cm and height, h = 7 cm. Find the volume of the cone

Solution: By making use of the formula of volume of the cone, we find,

V = ⅓ πr²h

So, V = ⅓ × 22/7 × 4² × 7

Therefore, V = 117.33 cm³

Question 5: A cone has a radius of 3 cm and a height of 5 cm? What is the total surface area of the cone?

Solution: By making use of the formula of the surface area of the cone, we know,

Area = π r(l + r)

Here, slant height l = √(r²+h²) = √(3²+5²) = √(9+25) = √34

So,

Area, A = π × 3(√34 + 3)

So, π × 3(5.83 + 3) = π × 3(8.83) = 83.22 Cm²

Therefore the total surface area of the cone is 83.22 cm²

Important Chapters:

• NCERT Solutions for Maths


• NCERT Solution for Class 9 Maths Chapter Coordinate Geometry


• NCERT Solution For Class 9 Maths Chapter Surface Area And Volume


• NCERT Solution For Class 10 Maths Chapter Surface Area And Volume


• NCERT Solution for Class 10 Maths Chapter Coordinate Geometry