
S1,S2 and S3 are the different sizes of windows 1,2 and 3 respectively placed in avertical plane. A particle is thrown up in that vertial plane, find the correct options:
average speed of the particle passing the windows may be equal if S1<S2<S3
average speed of the particle passing the windows may be equal if S1>S2>S3
if S1=S2=S3, the change in speed of the particle while crossing the windows will satisfy ΔV1<ΔV2<ΔV3.
if S1=S2=S3 the time taken by particle to cross the windows will satisfy t1<t2<t3
The correct Answer is:B, C, D
As going up, speed of the particle is decreasing and hence time taken in crossing the windows
(if S1=S2=S3) will be t1<t2<t3 since, →v=→u+→atΔu∝t (as acceleration is same)
So, Δv1<Δv2<Δv3 (as for equal windows t1<t2<t3) for unequal windows. t1=t2=t3 if S3<S2<S1
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Integer Type Question
13 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Single Answer Question
8 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Passage Type Questions
16 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)
31 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
Similar Questions
Knowledge Check
W1,W2 and W3 are the different sizes of windows 1,2, and 3 respectively placed in a vertical plane. A particle is thrown up in the vertical plane. Let t1,t2 and t3 are the time taken to cross the window W1,W2 and W3 respectively and ΔV1,ΔV2 and ΔV3 are the change in speed after respective window cross.
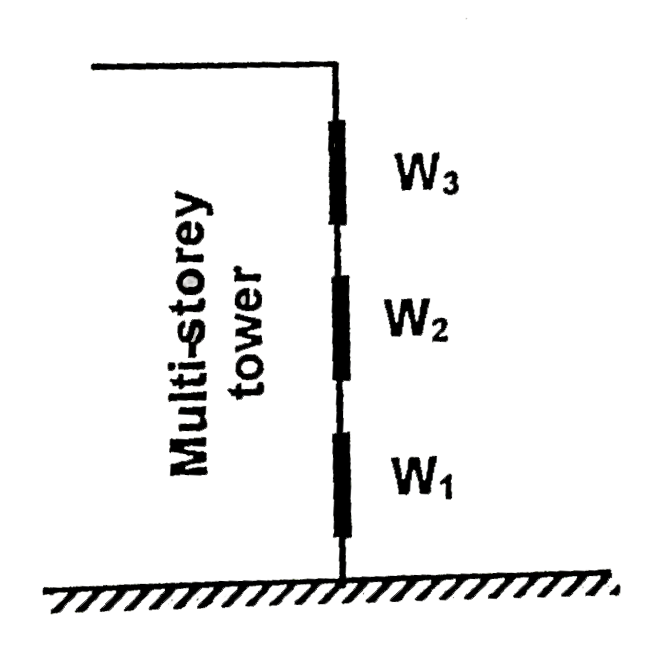 AAverage speed of the particle passing the windows may be equal if W1<W2<W3BAverage speed of the particle passing the windows may be equal if W1>W2>W3CIf W1=W2=WP3, the change in speed of the particle while crossing the windows will satisfy ΔV1<ΔV2<ΔV3DIf W1=W2=W3, the time taken by particle to cross the windows will satisfy t1<t2<t3
AAverage speed of the particle passing the windows may be equal if W1<W2<W3BAverage speed of the particle passing the windows may be equal if W1>W2>W3CIf W1=W2=WP3, the change in speed of the particle while crossing the windows will satisfy ΔV1<ΔV2<ΔV3DIf W1=W2=W3, the time taken by particle to cross the windows will satisfy t1<t2<t3If S1,S2,S3 be the sum of n, 2n, 3n terms respectively of an A.P., then
AS3=S1+S2BS3=2(S1+S2)CS3=3(S2−S1)Dnone of theseIf S1,S2,S3 are the sums of n, 2n, 3n terms respectively of an A.P., then S3/(S2−S1)−
A1B2C3D4
Let S1,S2,S3 be the respective sums of first n,2nand3n terms of the same arithmetic progression with a as the first term and d as the common difference. If R=S3−S2−S1, then R depends on
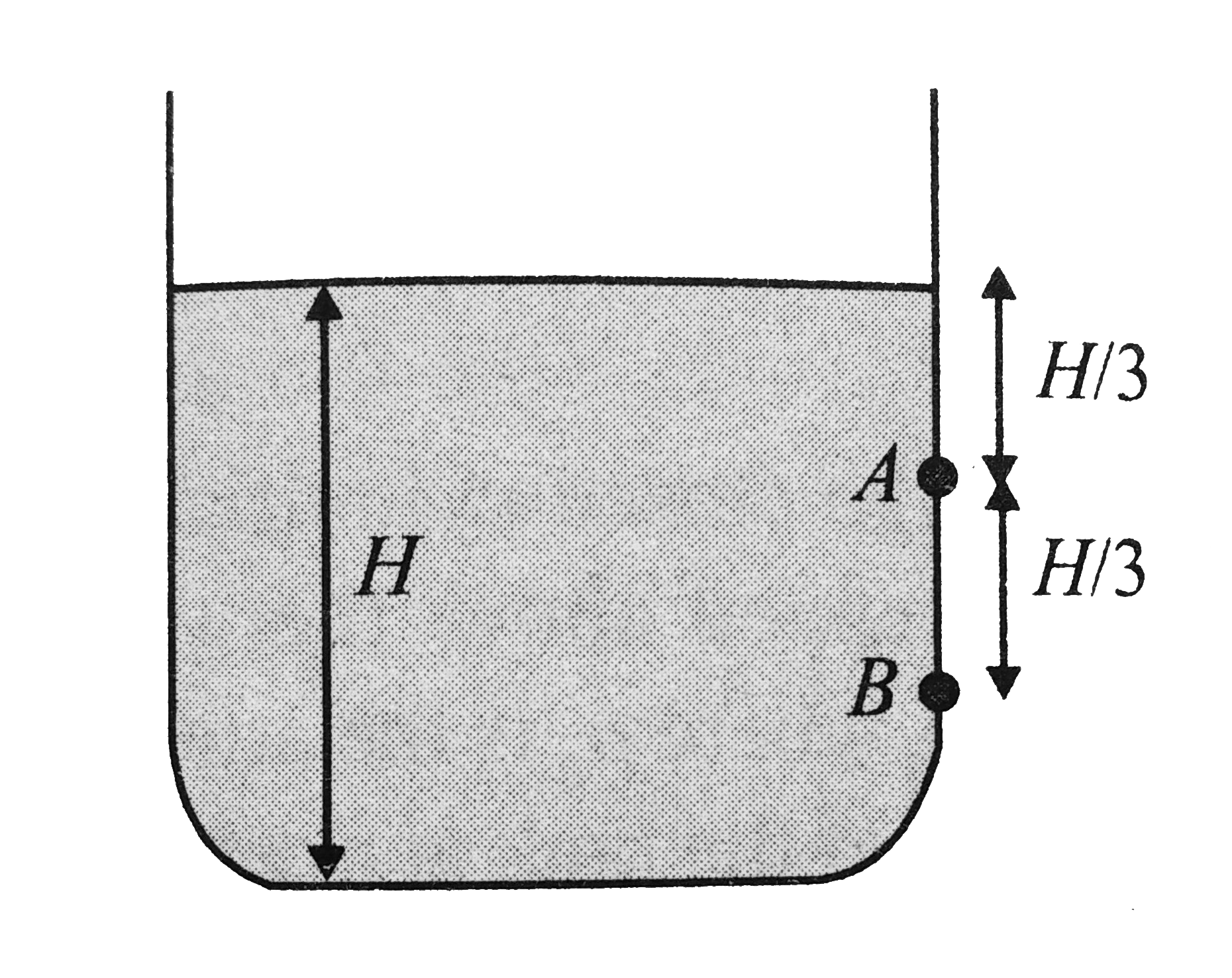
View SolutionThe area of two holes A and B are 2a and a, respectively, The holes are at height (H/3)and(2H/3) from the surface of water. Find the correct option(s):
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
P2 and P3 are images of each other with respect to the line
View SolutionLet a1,a2,a3,….,an be an A.P. and S1,S2andS3 be the sum of first n , 2n and 3n terms respectively then S3−S2−S1 is equal to , if a is first term and d is common difference :
View SolutionLet a1,a2,a3,….,an be an A.P. and S1,S2andS3 be the sum of first n , 2n and 3n terms respectively then S3−S2−S1 is equal to , if a is first term and d is common difference :
View Solution
