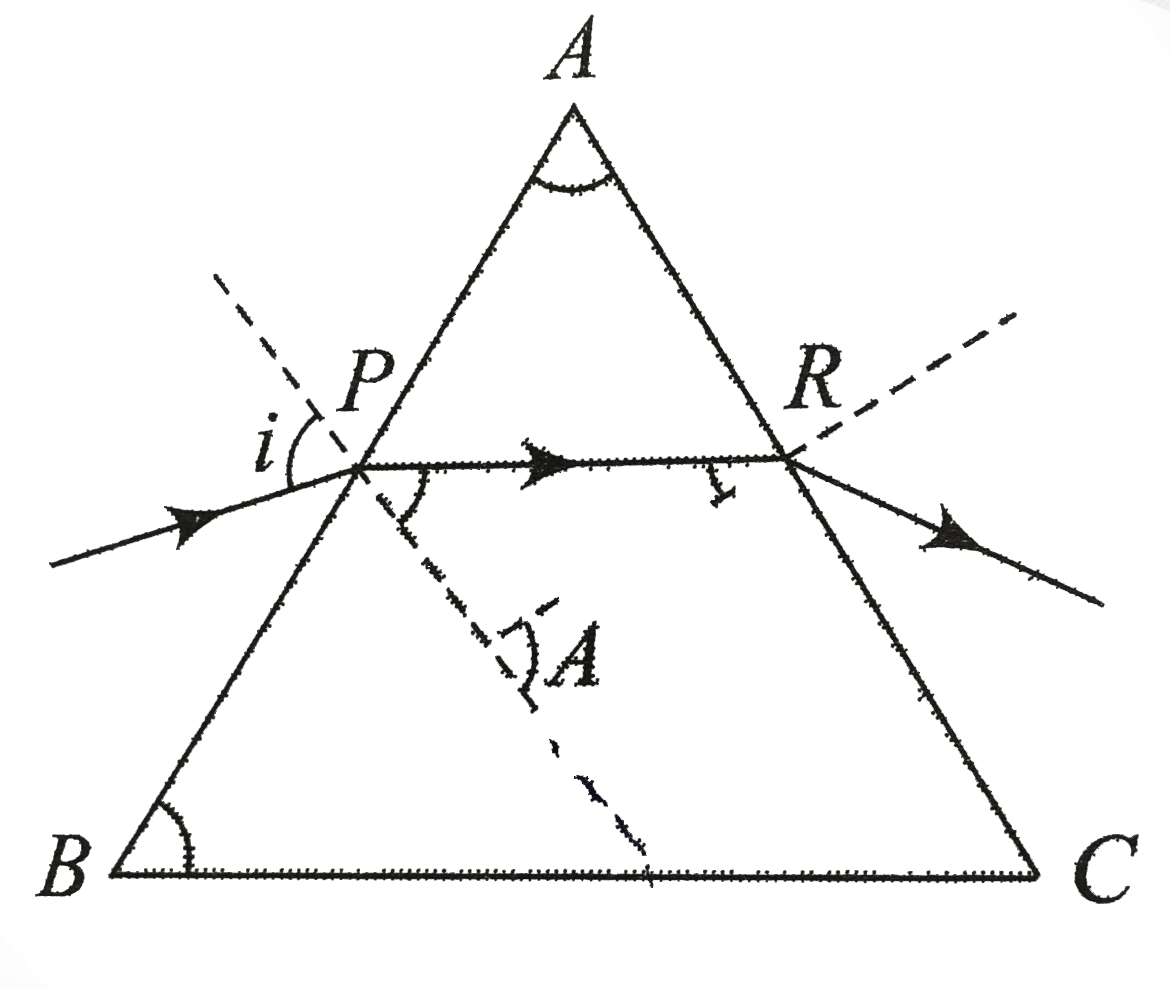
A ray of light undergoes deviation of $30^{\circ}$ when incident on an equilateral prism of refractive index $\sqrt{2} .$ what is the angle subtended by the ray inside the prism with the base of the prism?

Video Solution

Text Solution

Verified by Experts

$δ = 30^{\circ}$ , $A = 60^{\circ}$ , $μ = \sqrt{2}$
Let us first calculate $δ_{m}$
$μ = \frac{sin (\frac{A + δ_{m}}{2})}{sin (A / 2)}$
$\sqrt{2} = \frac{sin (\frac{60^{\circ} + δ_{m}}{2})}{{sin 30}^{\circ} = 1 / 2}$
$sin (\frac{60^{\circ} + δ_{m}}{2}) = \frac{1}{\sqrt{2}} = {sin 45}^{\circ}$
$\frac{60^{\circ} + δ_{m}}{2} = 45^{\circ}$
$δ_{m} = 30^{\circ} = δ$
Since $δ = δ_{m}$ , i.e. ray inside the prism is parallel to the base of the prism.

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ray of light undergoes deviation of $30^{\circ}$ when incident on an equilateral prism of refractive index $\sqrt{2}$ . The angle made by the ray inside the prism with the base of the prism is
A $15^{\circ}$
B $0^{\circ}$
C $45^{\circ}$
D $30^{\circ}$
Question 2 - Select One
A ray of light suffers minimum deviation when incident on an equilateral prism of refractive index $\sqrt{2}$ . What is the angle of incidence ?
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
Question 3 - Select One
A ray of light suffers a minimum deviation when incident on an equilateral prism of refractive index $\sqrt{2}$ The angle of incidence is
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $50^{\circ}$

CP SINGH-REFRACTION OF LIGHT BY PLANE SURFACES-Exercises

Home
Ask Doubt
Profile