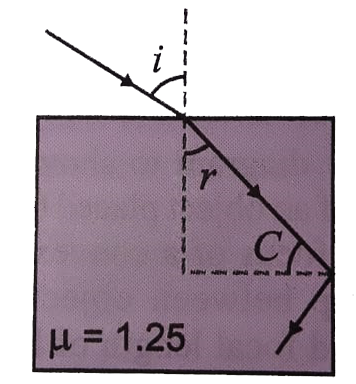
Consider the situation shown in figure. Find the maximum angle theta for which the light suffers total internal reflection at the vertical surface.
Video Solution
Text Solution

At AC:
1×sinθ=54sinθ′
sinθ′=45sinθ (i)
θ′+θ''=90∘ i.e. θ''=90∘−θ′ (ii)
μ2sinC=μ1sin90∘
sinC=μ1μ2=15/4=45 (iii)
For T.I.R. on AB
θ''≥C
sinθ''≥sinC
sin(90∘−θ′)≥sinC
cosθ′≥sinC
cos2θ′≥sin2C
1−sin2θ′≥sin2C
1−(45)2sin2θ≥(45)2
sin2θ≤[(54)2−1=(34)2]
sinθ≤34
θ≤sin−1(3/4)
θmax=sin−1(3/4)
|
Topper's Solved these Questions
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- SEMICONDUCTORSBOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises
140 Videos
Similar Questions
Knowledge Check
Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is.
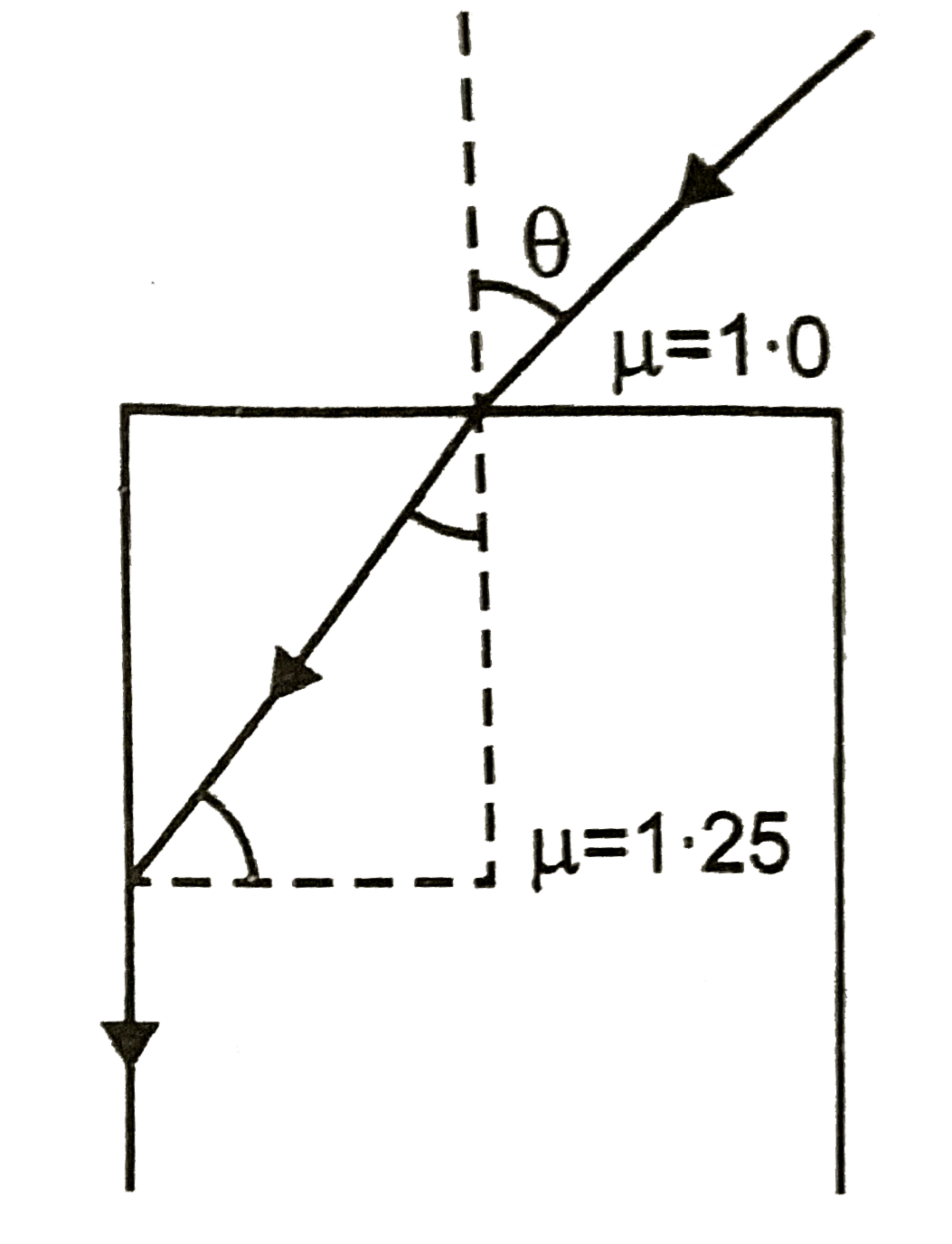 .Acos−1(34)Bsin−1(34)Ctan−1(43)Dcot−1(43)
.Acos−1(34)Bsin−1(34)Ctan−1(43)Dcot−1(43)Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is
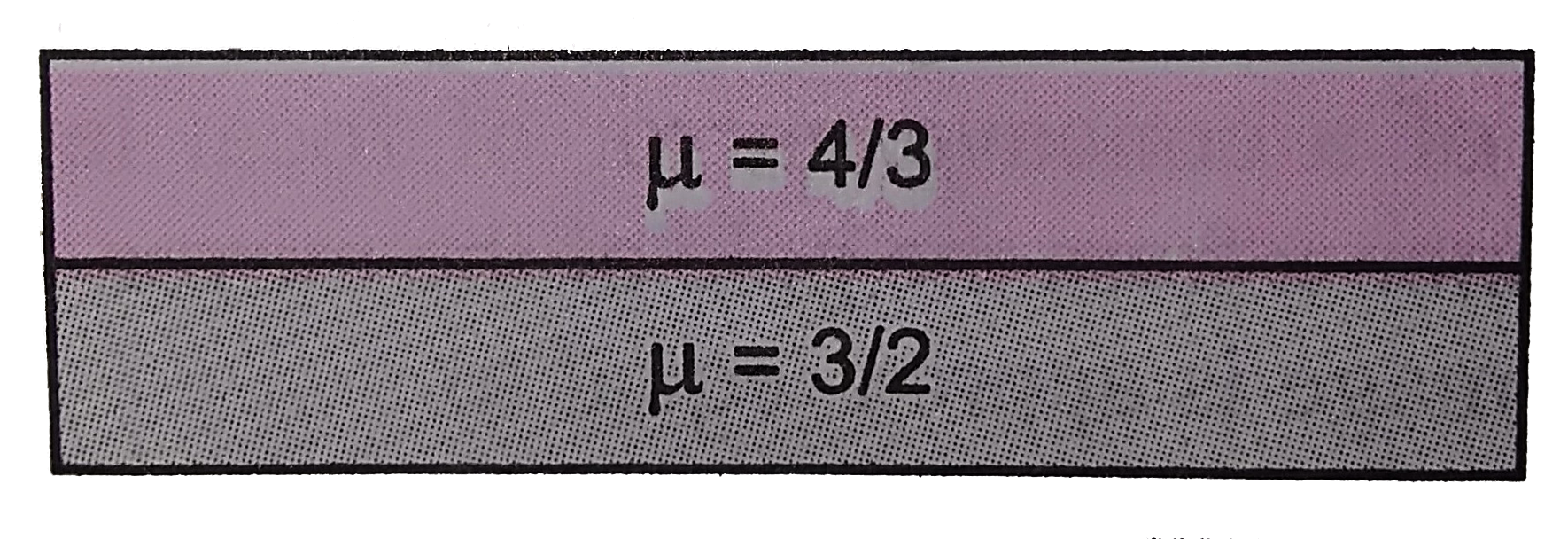 Acos−1(34)Bsin−1(34)Ctan−1(34)Dcot−1(34)
Acos−1(34)Bsin−1(34)Ctan−1(34)Dcot−1(34)For a situation shown in figure, find the refrective index of glass so that it will suffer total internal reflection at the vertical surface.
 A1.732B1.5C1.31D1.6
A1.732B1.5C1.31D1.6
Total internal reflection and critical angle
View SolutionDefine total internal reflection of light.
View SolutionConsider the situation shown in the figure.
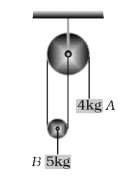
Find acceleration of A.
View SolutionConsider the situation shown in the figure.
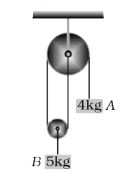
Find acceleration of B.
View SolutionFor total internal reflection, light must travel
View Solution

 .
.