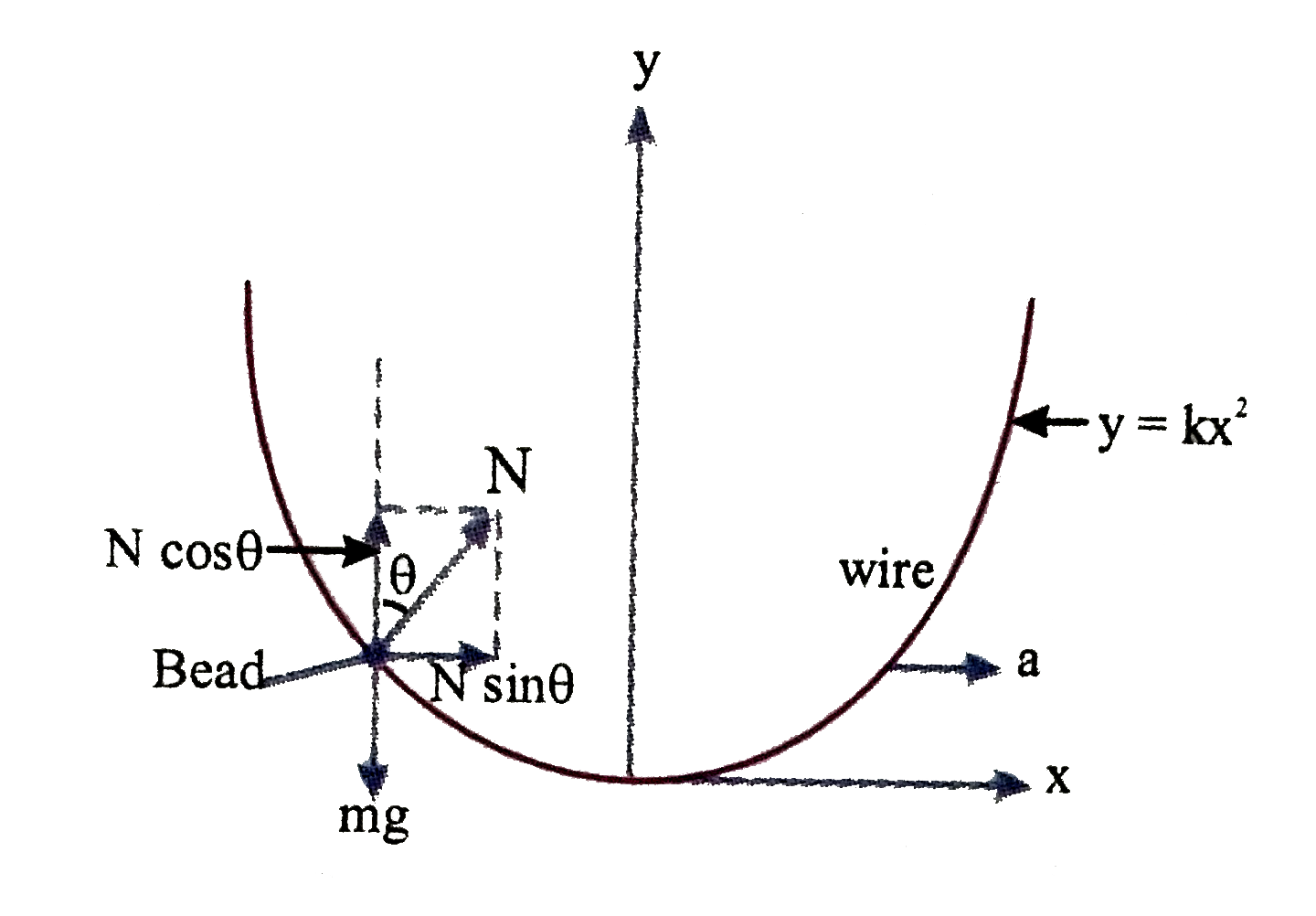
A piece of wire is bent in the shape of a parabola (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is
The correct Answer is:B
For the bead to stay at rest,
Which give , Now
slope of the curve =
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL I(H.W)
43 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)
51 Videos
- CIRCULAR MOTIONBOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL-VI Integer
7 Videos
- CALORIMETRYBOOK - NARAYNACHAPTER - CALORIMETRYEXERCISE - Level- II (H.W)
11 Videos
- COLLISIONBOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)
54 Videos
Similar Questions
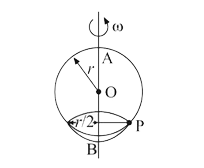
A smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
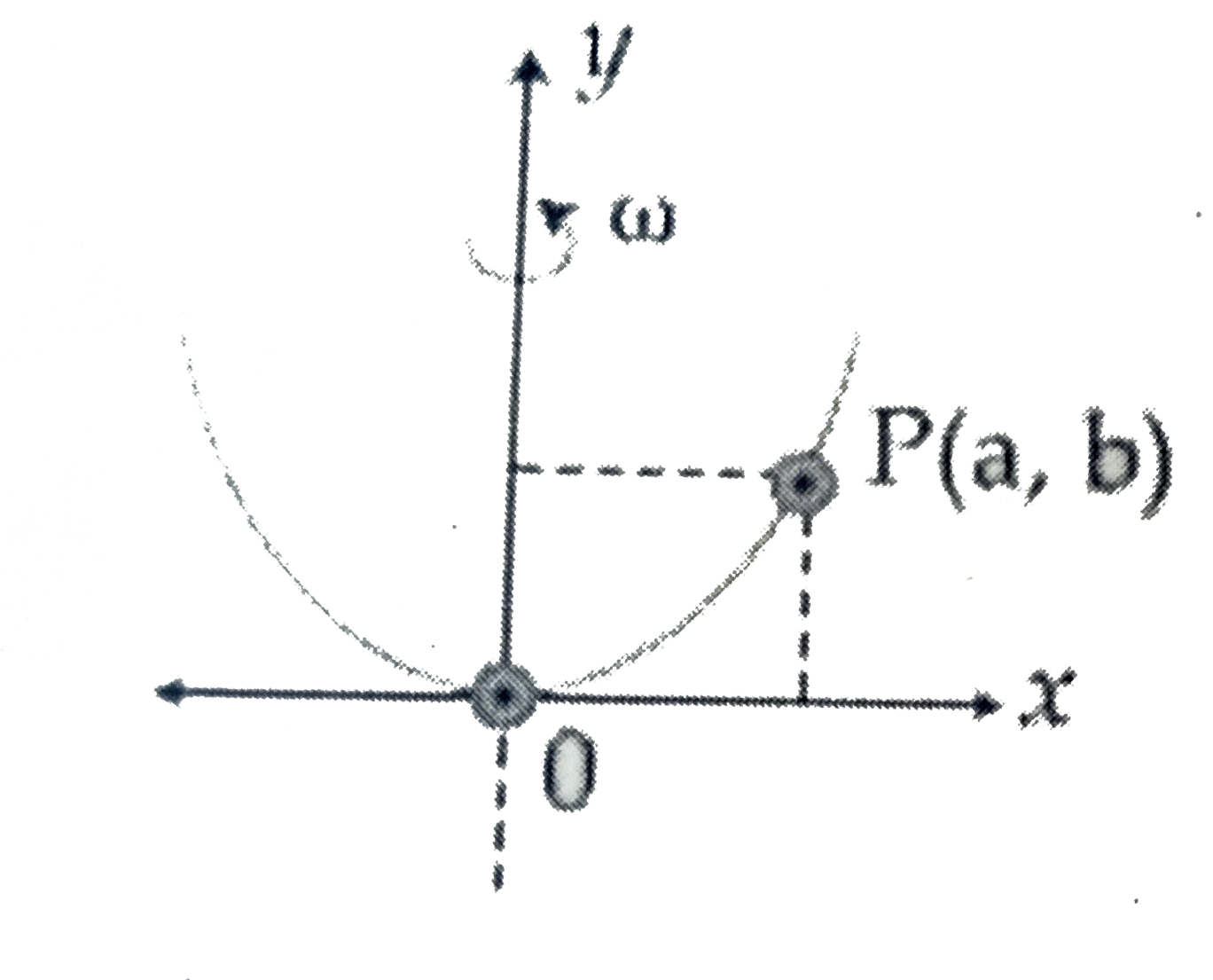
View SolutionA bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y=4Cx2 and rotating with angular speed ω (see figure ) . The value of ω is (neglect friction),
View Solution
Knowledge Check
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
AagkBa2gkC2agkDa4gkA wire which is bent in the shape of a curve given by, y=a3x4. A bead of mass m is located at point P(x,y). If the wire is smooth, find ω with which wire needs to be rotated for bead to be static.
Aa√x3gB2a√x3gC2x√a3gDx√a3gA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :
 Ag2B(√3g)(2)Cg√2Dg
Ag2B(√3g)(2)Cg√2Dg
A rigid mass less rod of length L is rotating in a vertical plane about a horizontal axis passing through one of its ends. At the other end of the rod there is a mass less metal plate welded to the rod. This plate supports a heavy small bead that can slide on the rod without friction. Just above the bead there is another identical metal plate welded to the rod. The bead remains confined between the plates. The gap between the plates is negligible compared to L. The angular speed of the rod when the bead is at lowest position of the circle is ω=2√gL. How many times a clink of the bead hitting a metal plate is heard during one full rotation of the rod ?

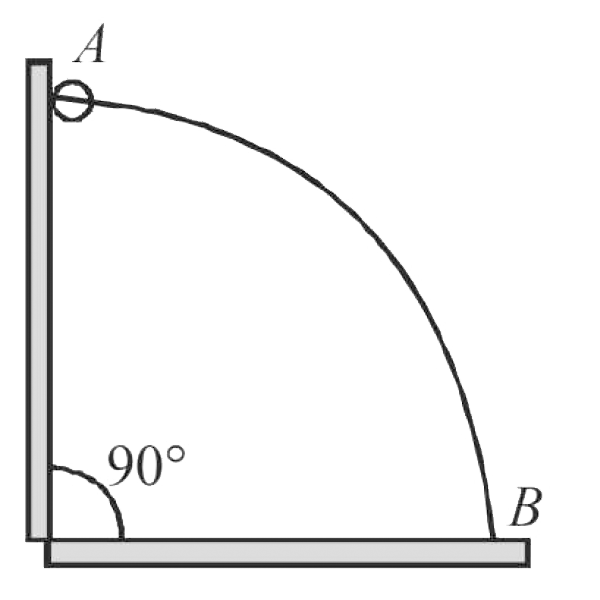
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View SolutionA straight wire carrying current is parallel to the y-axis as shown in Fig. The
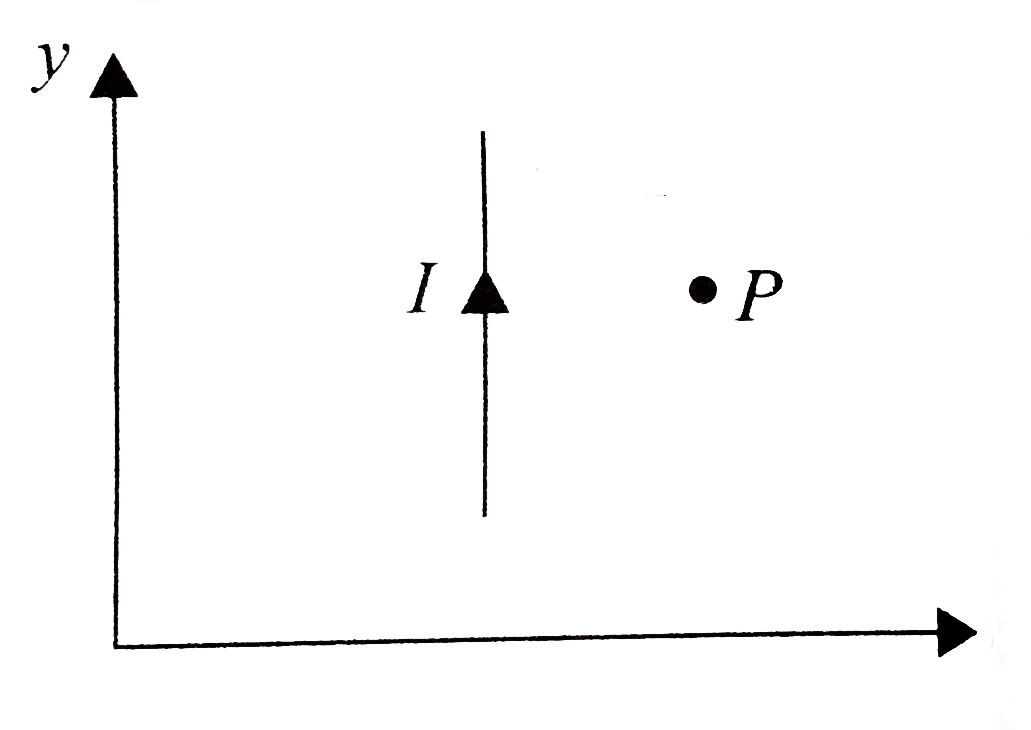
View SolutionAB is a light rigid rod. Which is rotating about a vertical axis passing through A,A spring of force constant K and natural length l is attached at A and its other end is attached to a small bead of mass m. The bead can slide without friction on the rod. At the initial moment the bead is at rest (w.rt. the rod) and the spring is unstreached Select correct option
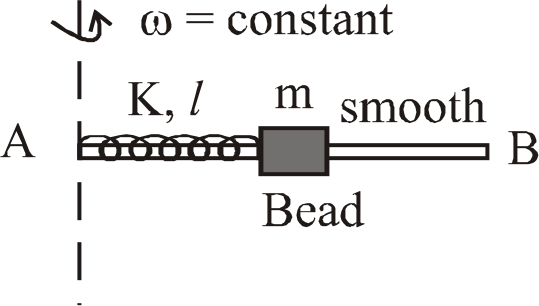
View SolutionAB is a light rigid rod. Which is rotating about a vertical axis passing through A,A spring of force constant K and natural length l is attached at A and its other end is attached to a small bead of mass m. The bead can slide without friction on the rod. At the initial moment the bead is at rest (w.rt. the rod) and the spring is unstreached Select correct option
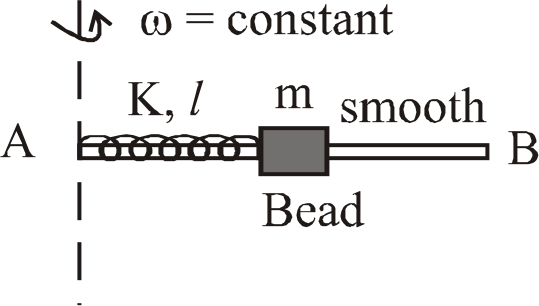
View Solution
