If a simple pendulum has significant amplitude (up to a factor of1//e of original) only in the period between $t - 0 s \to t = τ s$ , then $τ$ may be called the average life of the pendulum. When the sphetical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity with b as the constant of propotional to average life time of the pendulum is (assuming damping is small) in seconds:

Video Solution

Text Solution

Verified by Experts

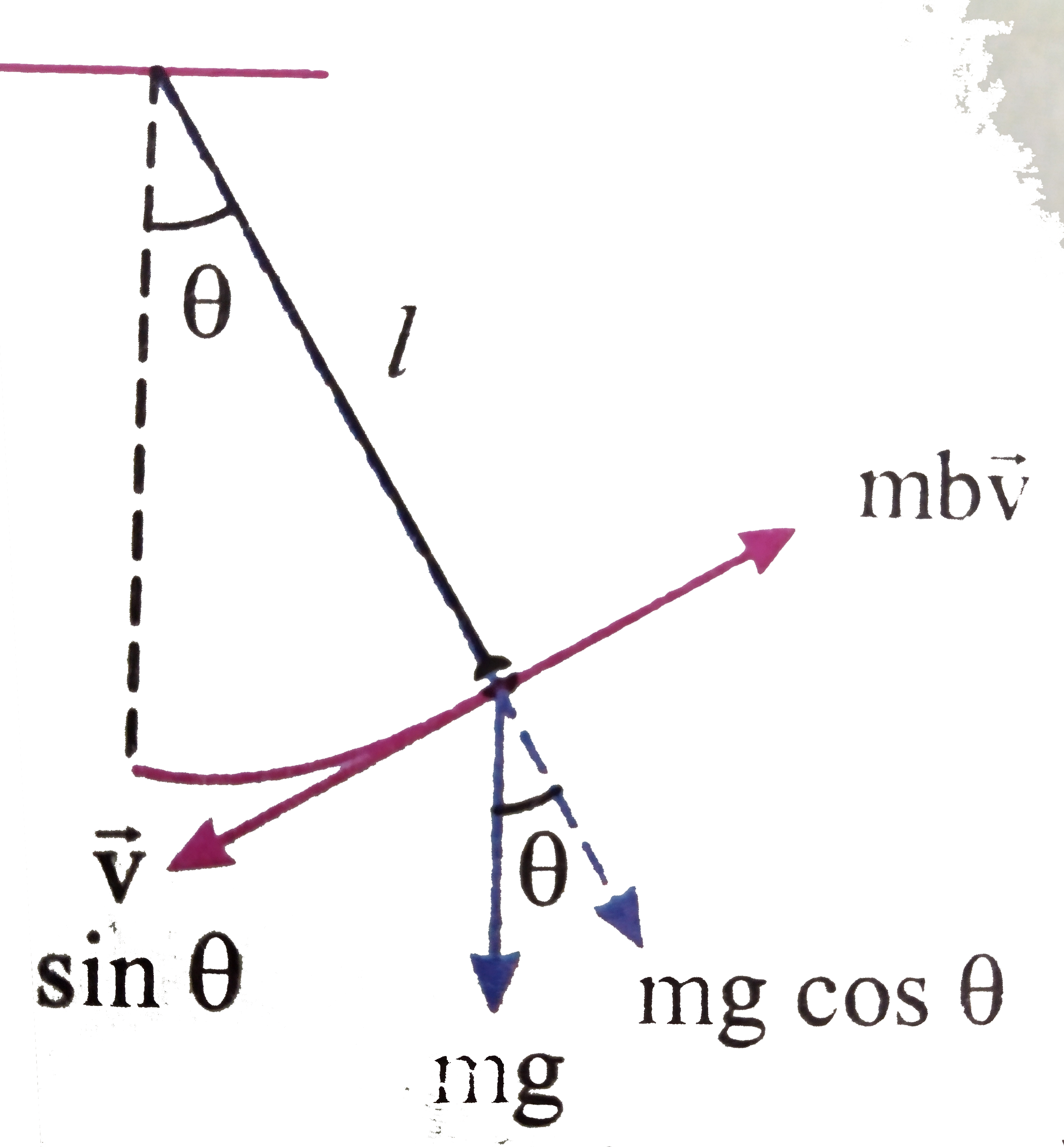
Retarding force $= m b v$ When angular displacement of the pendulum is $θ$ , net restroing torque $= - m g l sin θ + m b v l$ If $I$ is the moment of intertial of the pendulum about the point of suspension, then $I α = - m g l sin θ + m b v l$ Where $α = a n g . a .$
Now, as $I = m l^{2}, m l^{2} α = - m g l sin θ + m b v l$
$∴ α = \frac{d^{2} θ}{d t} = - \frac{g}{l} sin θ + \frac{b v}{l}$
For small damping, the solution of the above differential equation will be: $θ = θ_{0} e^{- b t / 2} sin (ω t + ϕ)$
$∴$ Angular amplitude $= θ_{0} e^{- b t / 2}$
According to question, in time $τ$ (average life time) angular amplitude reduces to $(1 / e)$ the value of the orginal value
$∴ \frac{θ_{0}}{e} = θ_{0} e^{- b t / 2}, \frac{b t}{2} = 1 or t = \frac{2}{b}$

Updated on:21/07/2023

The tension in the string of a simple pendulum is maximum, when the bob of the pendulum
Ais at the extreme position
Bmidway between the mean position and extreme position
Cis at the mean position
Dstarts oscillating with very large amplitudes
A simple pendulum is set into vibrations. The bob of the pendulum comes to rest after some time due t
AAir friction
BMoment of inertia
Cweight of the bob
DCombination of all the above
A simple pendulum has a time period T. If the support and the pendulum fall freely, the time period will be
Ainfinity
Bgreater than T
Cless than T
Dzero