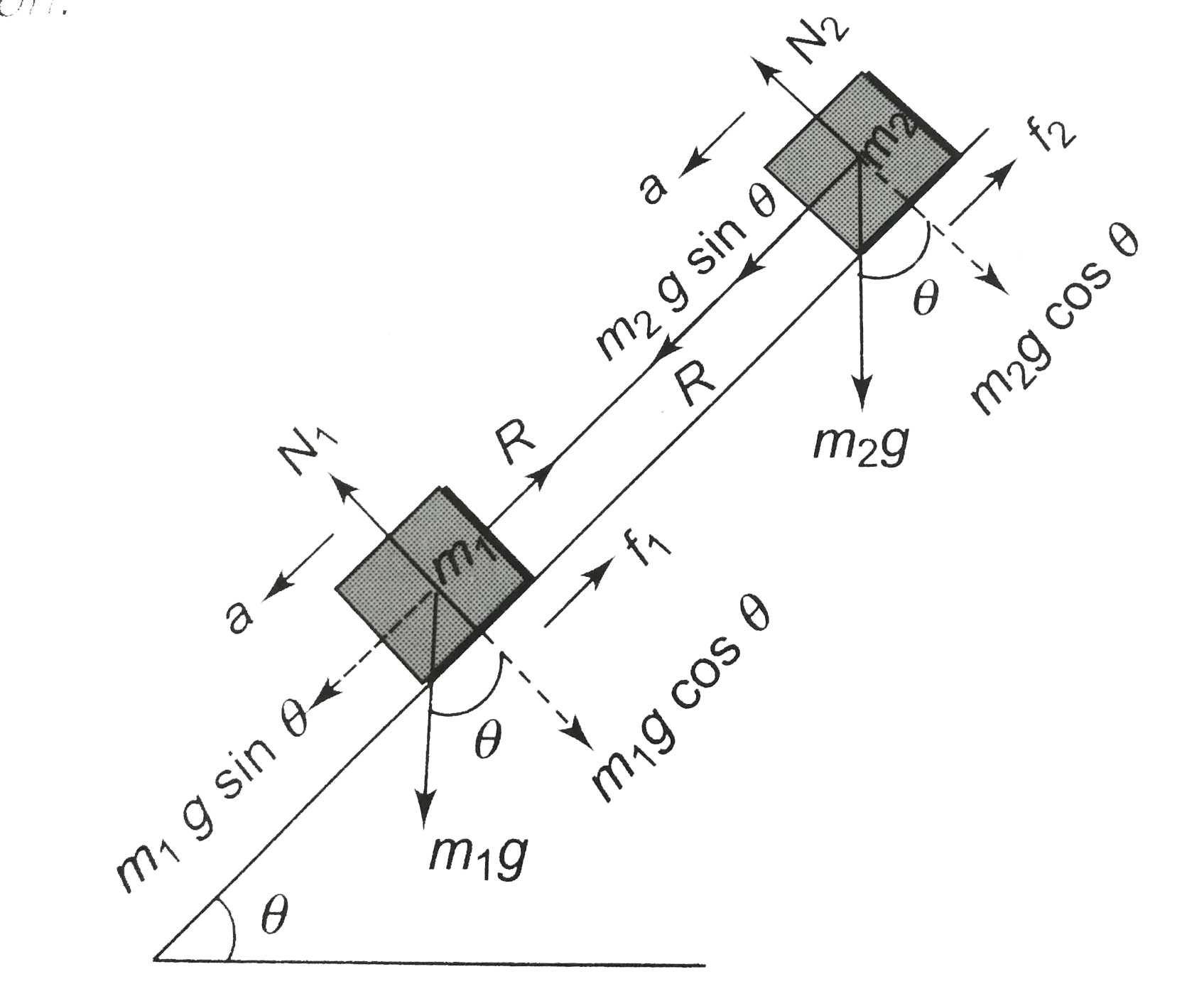
Two masses $M_{1} and M_{2}$ are connected by a light rod and the system is slipping down a rough incline of angle $θ$ with the horizontal. The friction coefficient at both the contacts is $μ$ . Find the acceleration of the system, and the force by the rod on one of the blocks.

Video Solution

Text Solution

Verified by Experts

Taking two blocks as system
$(m_{1} + m_{2}) g \sin θ - (f_{1} + f_{2}) = (m_{1} + m_{2}) a$
$f_{1} = μ N_{1} = μ m_{1} g \cos θ, f_{2} = μ N_{2} = μ m_{2} g a s θ$
$(m_{1} + m_{2}) g \sin θ - μ (m_{1} + m_{2}) g \cos θ = (m_{1} + m_{2}) a$
$a = g \sin θ - μ g \cos θ$
$m_{1} g \sin θ - R - f_{1} = m_{1} a$
$m_{1} (g \sin θ - μ g \cos θ) - R = m_{1} (g \sin θ - μ g \cos θ)$
$R = 0$

Updated on:21/07/2023

A block of mass m is placed on a rough plane inclined at an angle $θ$ with the horizontal. The coefficient of friction between the block and inclined plane is $μ$ . If $θ < {tan}^{- 1} (μ)$ , then net contact force exerted by the plane on the block is :
Amg cos $θ$
Bmg
Cmg sin $θ$
DNone of these
A solid cylinder of mass $m$ rolls without slipping down an inclined plane making an angle $θ$ with the horizontal. The frictional force between the cylinder and the incline is
A $m g sin θ$
B $\frac{m g sin θ}{3}$
C $m g cos θ$
D $\frac{2 m g sin θ}{3}$
A block of mass m slides down an inclined plane which makes an angle $θ$ with the horizontal. The coefficient of friction between the block and the plane is $μ$ . The force exerted by the block on the plane is
A $m g cos θ$
B $\sqrt{μ^{2} + 1} m g cos θ$
C $\frac{μ m g cos θ}{\sqrt{μ^{2} + 1}}$
D $μ m g θ$