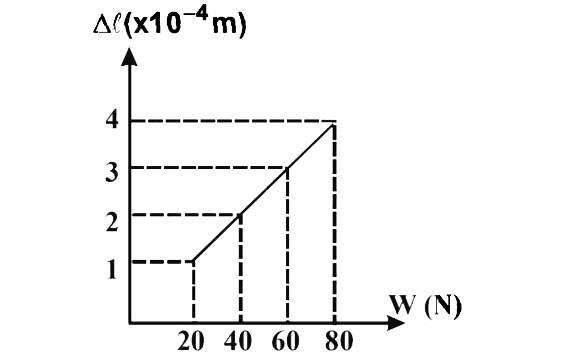
The adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .

2×1011N−m−2
2×10−11N−m−2
3×1012N−m−2
2×10−12N−m−2
The correct Answer is:A
Y=MgLA(ΔL)=WLA(Δl)=WΔl(LA)
∴ The graph of ΔL against load (W) is a straight line
∴ΔLW is constant
∴WΔL=2010−4
∴Y=2010−4×110−6=20×1010=2×1011N/m2
Topper's Solved these Questions
- ELASTICITYBOOK - MARVEL PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Test Your Grasp - 5
15 Videos
- CURRENT ELECTRICITYBOOK - MARVEL PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - MCQ
151 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS EXERCISE - TEST YOUR GRASP - 16
30 Videos
Similar Questions
The adjacent graph shows the extra extension (Δx) of a wire of length 1m suspended from the top of a roof at one end with an extera load Δw connected to the other end If the cross sectional area of the wire is 10−5m2 calculate the Young's modulus of the meterial of the wire
(A) 2×1011N/m2 (B) 2×10−11N/m2 (c) 3×10913)N/m3 (D) 2×1016N/m2
 .
.
View Solution_S01_065_Q01.png)
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the young's modulus of the material of the wire is
(a). 2×1011Nm−2
(b). 2×1010Nm−2
(c). 12×1011Nm−2
(d). none of these
View Solution
Knowledge Check
The adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
 A(a) 2×1011N/mB(b) 2×10−11N/mC(c) 3×10−12N/mD(d) 2×10−13N/m
A(a) 2×1011N/mB(b) 2×10−11N/mC(c) 3×10−12N/mD(d) 2×10−13N/mA wire of length 10 m and cross-section are 10−6m2 is stretched with a force of 20 N. If the elongation is 1 mm, the Young's modulus of material of the wire will be
A1010N/m2B1011N/m2C2×1010N/m2D2×1011N/m2A load of 3kg produces an extension of 1.5mm in a wire of length 3m and diameter 2mm. Young's modulus of the material of the wire is
A1.87×1010Nm−2B3.5×1010Nm−2C15×1010Nm−2D2.5×1010Nm−2
The graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the Young's modulus of the material of the wire.

View SolutionA wire of length 1 m and area of cross section 2×10−6m2 is suspended from the top of a roof at one end and a load of 20 N is applied at the other end. If the length of the wire is increased by 0.5×10−4m, calculate its Young’s modulus (in 1011N/m2).
View SolutionA wire of 10m long and 1mm2 area of cross section is strechted by a force of 20N. If the elongation is 2mm the young's modulus of the material of the wire (in Pa) is
View SolutionA block of mass 500kg is suspended by wire of length 70 cm. The area of cross-section of wire is 10 mm2. When the load is removed, the wire contracts by 0.5cm. The young's modulus of the material of wire will be
View SolutionA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the torce corstant of the wire is
View Solution
