A wheel rotates about an axis passing through the center and perpendicular to the plane with slowly increasing angular speed. Then it has

tangential velocity and radial acceleration

radial velocity and radial acceleration

tangential velocity and tangential and radial accelerations

Tangential velocity and tangential acceleration

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

AS the angular speed of the wheel is slowly increased , it has an angular acceleration $α$ and tangential acceleration $a_{T} = γ α .$ Similarly it has a radial acceleration $a_{R} .$ Thus it has $v_{T}, a_{T} and a_{R}$ .

Updated on:21/07/2023

Class 12 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Knowledge Check

A disc of the moment of inertia $' l_{1}'$ is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed $' ω_{1}'$ . Another disc of moment of inertia $' I_{2}'$ . having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed $' ω_{2}'$ . The energy lost by the initial rotating disc is
A $\frac{1}{2} [\frac{l_{1} + l_{2}}{l_{1} l_{2}}] ω_{1}^{2}$
B $\frac{1}{2} [\frac{l_{1} l_{2}}{l_{1} - l_{2}}] ω_{1}^{2}$
C $\frac{1}{2} [\frac{l_{1} - l_{2}}{l_{1} l_{2}}] ω_{1}^{2}$
D $\frac{1}{2} [\frac{l_{2} l_{2}}{l_{1} + l_{2}}] ω_{1}^{2}$
In figure, there is conducting ring having resistance $R$ placed in the plane of paper in a uniform magnetic field $B_{0}$ . If the rings is rotating in the plane of paper about an axis passing through point $O$ and perpendicular to the plane of paper with constant angular speed $ω$ in clockwise direction, then

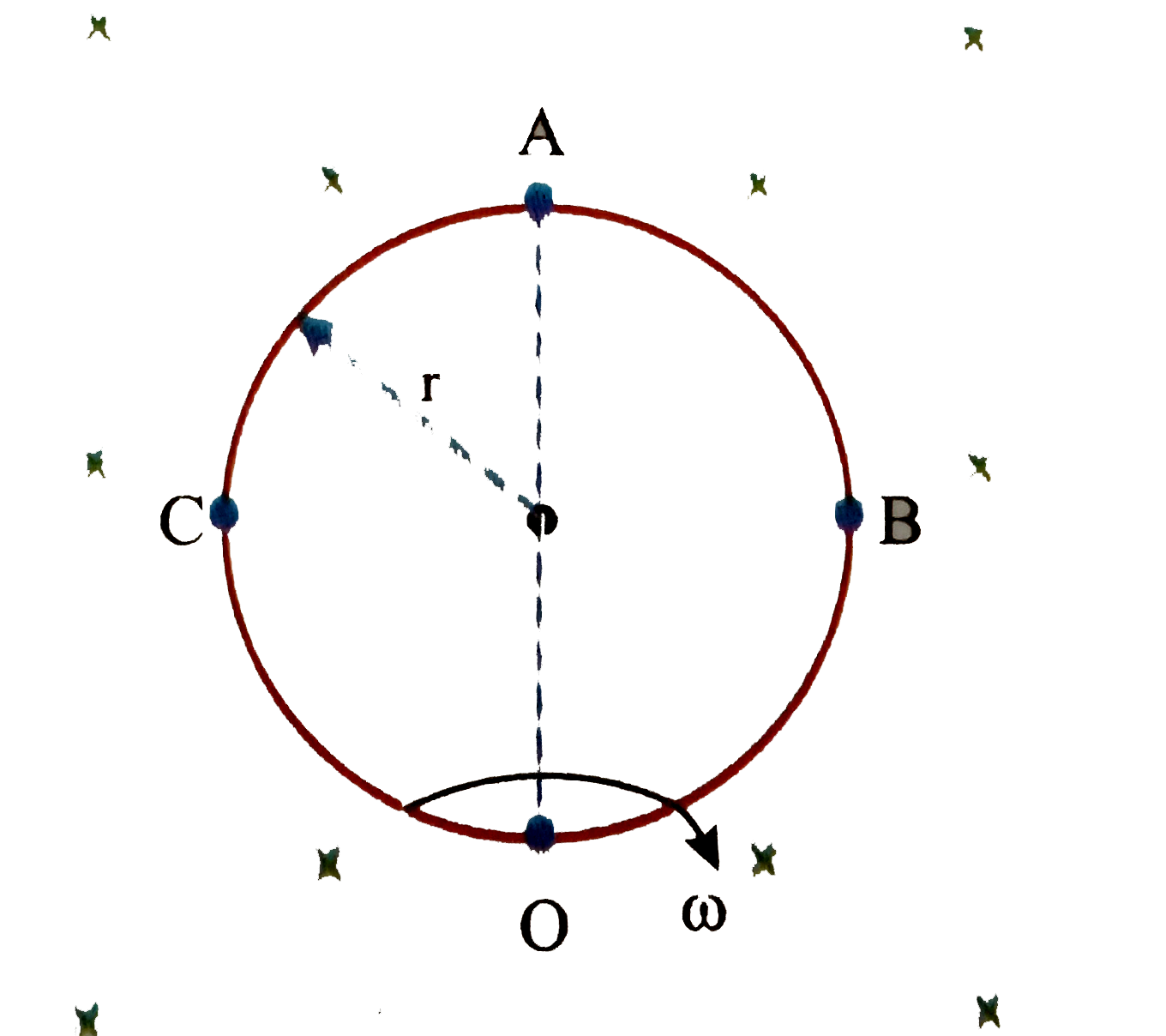Apoint $O$ will be at higher potential than $A$
Bthe potential of point $B$ and $C$ will be different
Cthe current in the ring will be zero
Dthe current in the ring will be $2 B_{0} ω r^{2} / R$
If two disc of moment of inertia $l_{1}$ and $l_{2}$ rotating about collinear axis passing through their centres of mass and perpendicular to their plane with angular speeds $ω_{1}$ and $ω_{2}$ respectively in opposite directions are made to rotate combinedly along same axis, then the magnitude of angular velocity of the system is
A $\frac{l_{1} ω_{1} + l_{2} ω_{2}}{l_{1} + l_{2}}$
B $\frac{l_{1} ω_{1} - l_{2} ω_{2}}{l_{1} + l_{2}}$
C $\frac{l_{1} ω_{1} + l_{2} ω_{2}}{ω_{1} + ω_{2}}$
D $\frac{l_{1} ω_{1} - l_{2} ω_{2}}{ω_{1} - ω_{2}}$

MARVEL PUBLICATION-CIRCULAR MOTION-TEST YOUR GRASP-20

Home
Ask Doubt
Profile