A particle is moving in a circular path with a constant speed. If θ Is the angular displacement, then starting from θ=0 , the maximum and minimum change in the linear momentum will occur when value of θ is respectively
A
0∘and90∘
B
90∘and180∘
C
180∘and270∘
D
180∘and360∘
Video Solution
Text Solution
The correct Answer is:D
When θ=180∘
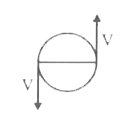
Change in monentum =mv−(−mv)=2mv
This is maximum . When it will return to its intial position θ=360∘ , and change in momentum =mv−mv=0.
this is minimum
|
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-1
1 Videos
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-2
1 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - MARVEL PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - TEST YOUR GRASP
30 Videos
- COMMUNICATION SYSTEMS BOOK - MARVEL PUBLICATIONCHAPTER - COMMUNICATION SYSTEMS EXERCISE - TEST YOUR GRASP -20
10 Videos
Similar Questions
Knowledge Check
A particle is moving in a circular path with a constant speed. If θ Is the angular displacement, then starting from θ=0 , the maximum and mimnimum change in the linear momentum will occur when nvalue of θ is respectively
A45∘ and 90∘B90∘ and 180∘C180∘ and 360∘D90∘ and 270∘For a particle moving along a circular path with a constant speed, the accelerationis constant in
Amagnitude onlyBdirection onlyCboth magnitude and directionDneither magnitude nor directionA particle is moving on a circular path with a constant speed 'v'. Its change of velocity as it moves from A to B is:
 A2vsinθBvsinθ/2CvcosθD2vsinθ/2
A2vsinθBvsinθ/2CvcosθD2vsinθ/2
A particle moves in a circular path with decreasing speed. What happens to its angular momentum ?
View SolutionWrite the maximum and minimum values of cosθ .
View SolutionA particle is going around in a circular path with constant speed. Angular momentum of particle is conserved about
View SolutionA particle moves in a circular path of radius 0.5 m with a linear speed of 2 ms−1 ,its angular speed is
View SolutionA particle is moving on a cicular path of radius 'R' . As it moves through an angular displacement θ, its linear displacement will be :
View Solution
