One mole of an ideal monoatmic gas undergoes a process defined y U=a√V where U is internal energy and V is its volume.The molar specific heat of the gas for this process is found to be ∗12R. The number in the numerator is not readable.What may be this number ?
25
21
41
42
The correct Answer is:D
To solve the problem, we need to determine the molar specific heat of an ideal monatomic gas undergoing a process defined by the equation U=A√V, where U is the internal energy and V is the volume. We are given that the molar specific heat for this process is expressed as ∗12R, and we need to find the value of the unknown numerator.
1. Understand the Relationship of Internal Energy and Temperature:
The internal energy U of an ideal gas is a function of temperature only. For a monatomic ideal gas, the internal energy can be expressed as:
U=nCvT
where Cv is the molar specific heat at constant volume.
2. Differentiate the Given Internal Energy Expression:
We have U=A√V. To relate this to temperature, we can differentiate both sides with respect to volume V:
dUdV=A2√V
3. Use the First Law of Thermodynamics:
The first law states that:
dU=δQ−δW
For an infinitesimal process, we can express δW as PdV (where P is pressure). Thus, we have:
δQ=dU+PdV
4. Express Heat Capacity:
The molar specific heat C for the process can be defined as:
C=δQdT
We can express δQ using the earlier relationship:
C=dU+PdVdT
5. Relate Pressure and Volume:
For an ideal gas, we have the equation:
PV=nRT
Thus, we can express P in terms of V and T:
P=nRTV
6. Substituting into the Heat Capacity Equation:
Substitute dU and P into the equation for C:
C=A12√VdV+nRTVdVdT
7. Finding the Relationship Between dT and dV:
Using the ideal gas law, we can find dT in terms of dV:
dT=RndVV
8. Final Expression for Molar Specific Heat:
After substituting and simplifying, we can find the specific heat C in terms of R and constants. Eventually, we find:
C=72R
9. Equate to Given Expression:
We are given that:
C=∗12R
Setting these equal gives:
∗12R=72R
Dividing through by R (assuming R≠0):
∗12=72
10. Solve for the Unknown Numerator:
Multiply both sides by 12:
∗=12⋅72=42
Conclusion:
The unknown number in the numerator is 42.
The internal energy U of an ideal gas is a function of temperature only. For a monatomic ideal gas, the internal energy can be expressed as:
U=nCvT
where Cv is the molar specific heat at constant volume.
We have U=A√V. To relate this to temperature, we can differentiate both sides with respect to volume V:
dUdV=A2√V
The first law states that:
dU=δQ−δW
For an infinitesimal process, we can express δW as PdV (where P is pressure). Thus, we have:
δQ=dU+PdV
The molar specific heat C for the process can be defined as:
C=δQdT
We can express δQ using the earlier relationship:
C=dU+PdVdT
For an ideal gas, we have the equation:
PV=nRT
Thus, we can express P in terms of V and T:
P=nRTV
Substitute dU and P into the equation for C:
C=A12√VdV+nRTVdVdT
Using the ideal gas law, we can find dT in terms of dV:
dT=RndVV
After substituting and simplifying, we can find the specific heat C in terms of R and constants. Eventually, we find:
C=72R
We are given that:
C=∗12R
Setting these equal gives:
∗12R=72R
Dividing through by R (assuming R≠0):
∗12=72
Multiply both sides by 12:
∗=12⋅72=42
The unknown number in the numerator is 42.
Topper's Solved these Questions
Similar Questions
An ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
View SolutionOne mole of a diatomic gas undergoes a thermodynamic process, whose process equation is P∝V2. The molar specific heat of the gas is
View Solution
Knowledge Check
An ideal gas with adiabatic exponent γ=43 undergoes a process in which internal energy is related to volume as U=V2 . Then molar heat capacity of the gas for the process is :
A3RB3.5RC4RDNone of theseOne mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
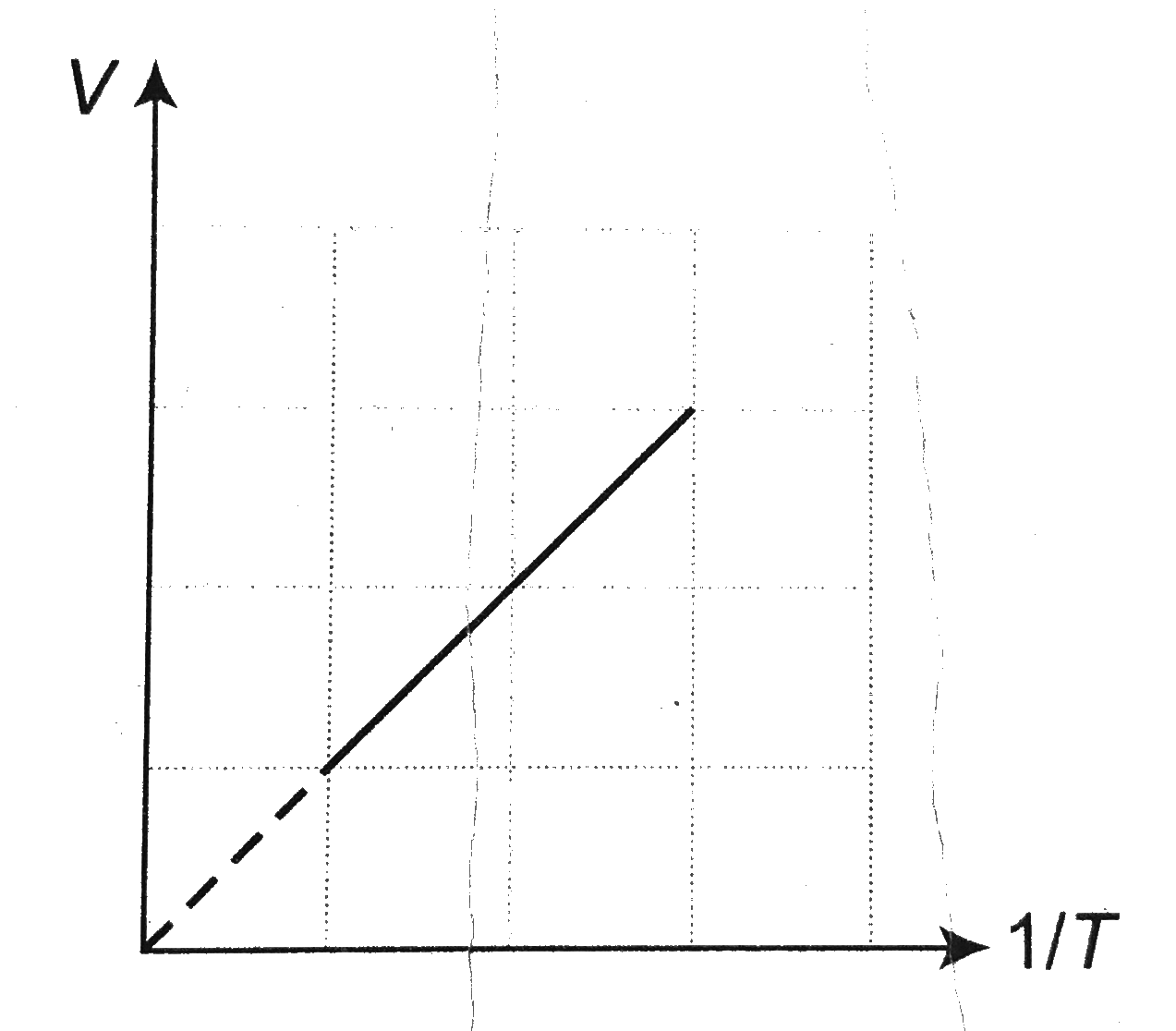
R is a gas constant.A3R4BR2CR3D2R3A certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
AR/2B−3R/2C3R/2D−R/2
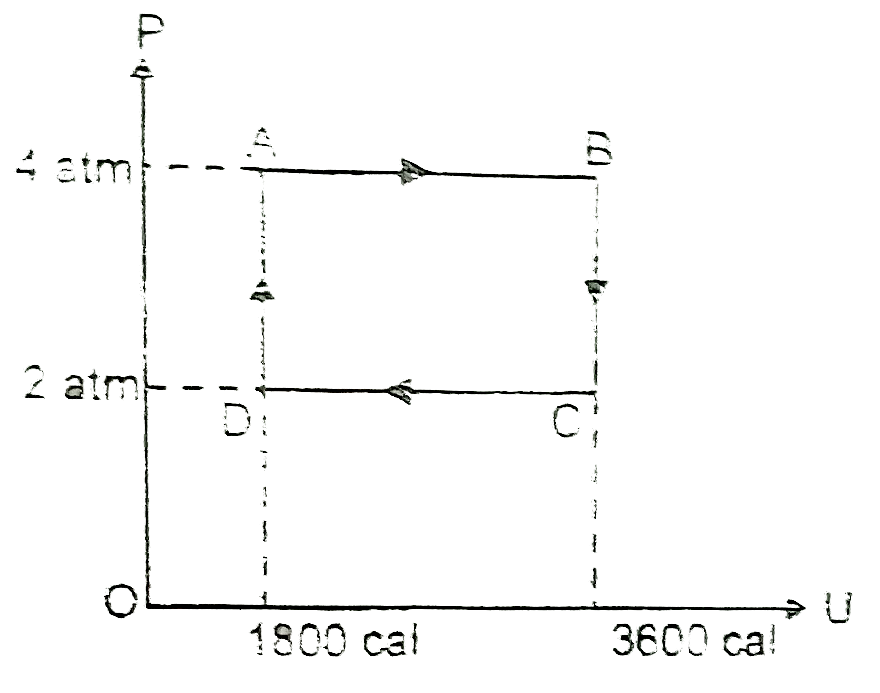
Two moles of an ideal monoatomic gas undergo a cyclic process which is indicated on a P−U diagram, where U is the internal energy of the gas. The work done by the gas in the cycle is k×102In2. Find k.
View SolutionOne mole of an ideal monotomic gas undergoes a linear process from A to B in which its pressure p and its volume V change as shown in figure.

The maximum temperature of the gas during this process is
View SolutionTempareture and volume of one mole of an ideal momatomic gas in a process are related as TV23=K ,where k is constant.The molar specific heat capacity for the process is
View SolutionAn ideal diatomic gas is expanded so that the amount of heat transferred to the gas is equal to the decrease in its internal energy.
The molar specific heat of the gas in this process is given by C whose value is
View SolutionOne mole of an ideal monoatomic gas undergoes a described by the equations PV3= constant The heat the gas during this process is :
View Solution
