
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
Consider a small element dx of the rod which is at a distance x from the end P if θ is the inclination of rod w.r.t the axis of rotation, the radius of the circle in which the element rotates is given by sinθ=rx⇒r=xsinθ
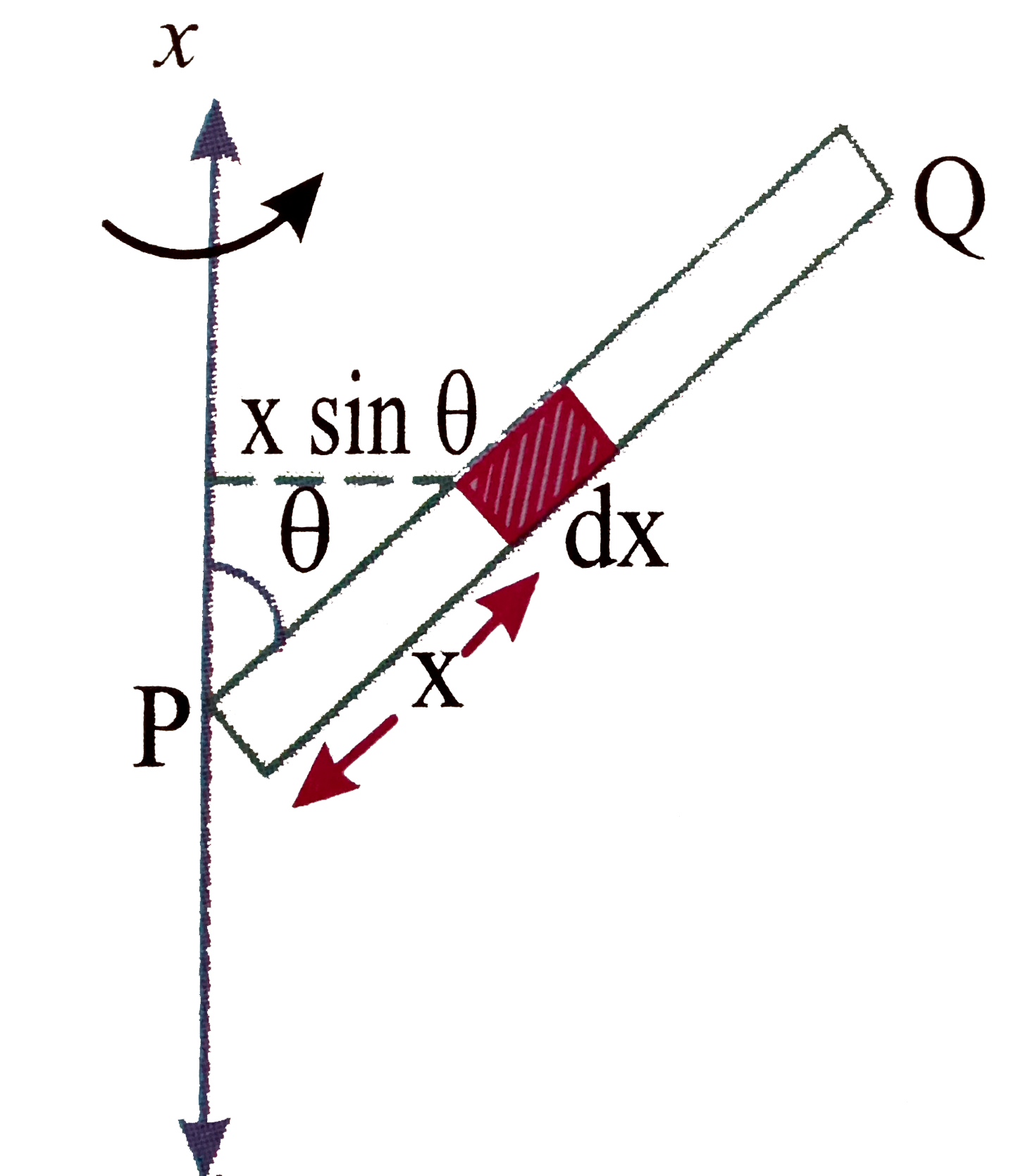
M.I. of the element about the axis of rotation is dI=dm.r2
where dmis the mass of element dm=mLdx
dI=mLdx(xsinθ)2. Total M.I. of the rod is given by I=∫dI=∫L0mLsin2θx2dx,I=mL23sin2θ
Similar Questions
A rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as ρ=ax2+b kg/m
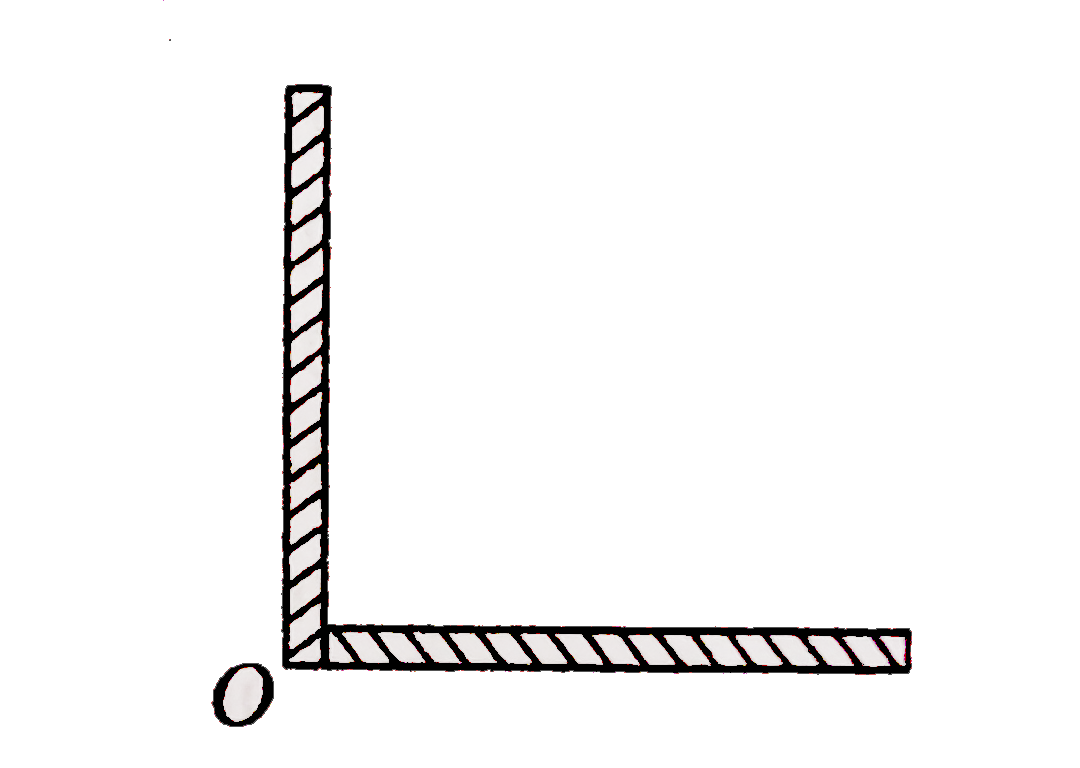
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
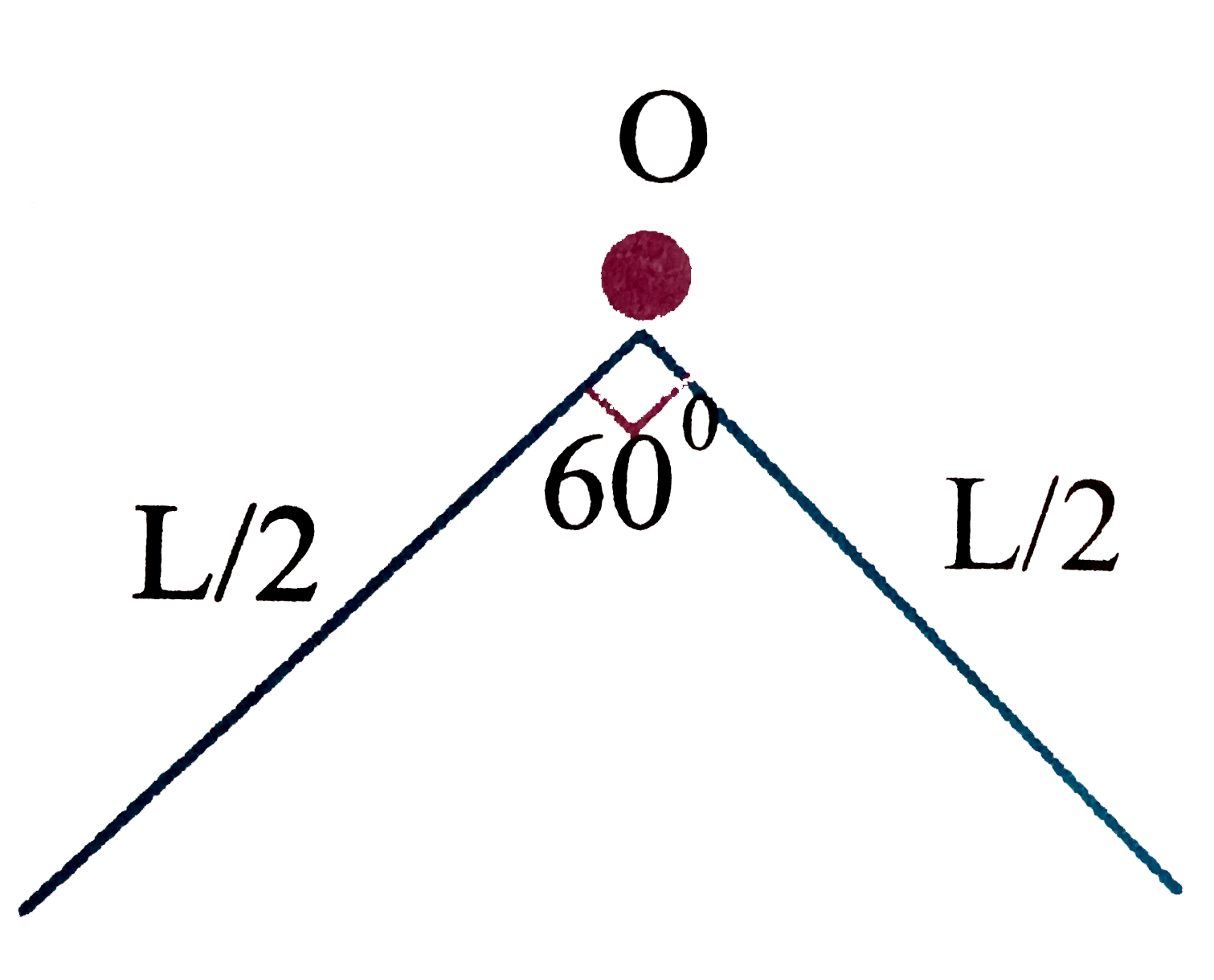
A thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
 AML26BML212CML224DML23
AML26BML212CML224DML23 - Question 2 - Select One
A thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
 AML26BML212CML224DML23
AML26BML212CML224DML23 - Question 3 - Select One
A thin rod of length l and mass m is turned at mid-point O at angle of 60°. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
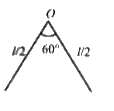 Aml2/3Bml26Cml28Dml212
Aml2/3Bml26Cml28Dml212
Two uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.
 View Solution
View SolutionA non-uniform rod AB has a mass M ad length 2l. The mass per unit length of the rod is mx at a point of the rod distant x from A. find the moment of inertia of this rod about an axis perpendicular to the rod (a) through A (b) through the mid-point of AB.
View SolutionA rod of length L is composed of a uniform length 1/2 L of wood mass is mw and a uniform length 1/2 L of brass whose mass is mb. The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
View SolutionTwo rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
View SolutionTwo rods each of mass m and length l are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them is :
View Solution

