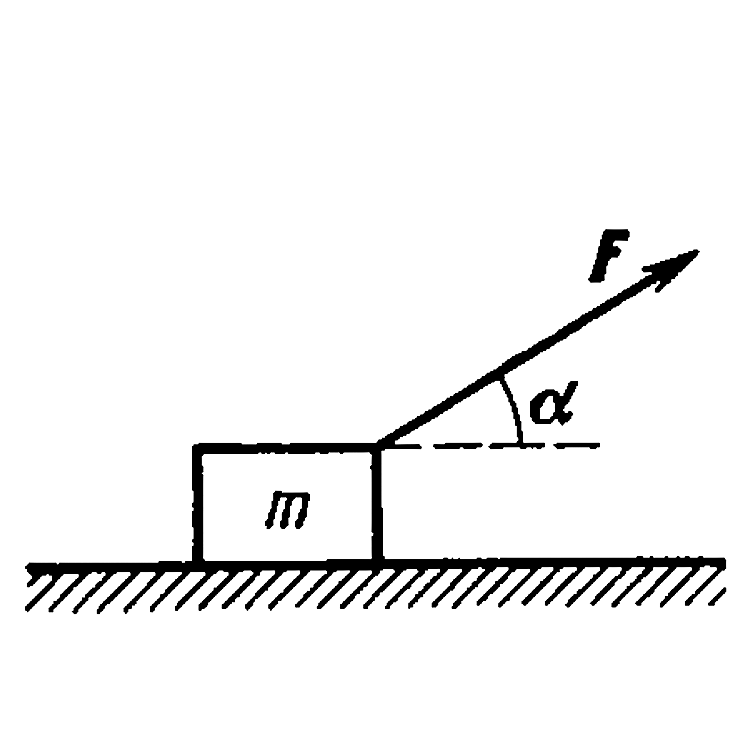
At the moment $t = 0$ the force $F = a t$ is applied to a small body of mass $m$ resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle $α$ with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.

A

$(\frac{m g^{2} cos θ}{2 c {sin}^{2} θ}) m / s, (\frac{m g^{3} c o n θ}{6 c^{2} {sin}^{3} θ}) m$

B

$(\frac{m g^{2} cos θ}{2 c {sin}^{2} θ}) m / s, (\frac{m^{2} g^{3} cos θ}{6 c^{2} {sin}^{3} θ}) m$

C

$(\frac{m g cos θ}{2 c {sin}^{2} θ}) m / s, (\frac{m^{2} g^{3} sin θ}{6 c^{2} {cos}^{3} θ}) m$

D

$(\frac{m g^{2} cos θ}{2 c {sin}^{2} θ}) m / s, (\frac{m^{2} g^{3} sin θ}{6 c^{2} {cos}^{3} θ}) m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Since $F$ $cos θ = m a$ or ct $cos θ = m \frac{d v}{d t}$
$v \int 0 d v = \frac{c cos θ}{m} t \int 0 t d t or v = (\frac{c cos θ}{2 m}) t^{2}$
But velocity at the time of breaking off or at
$t = \frac{m g}{c sin θ}$
$∴ v = \frac{c cos θ}{2 m} x {(\frac{m g}{c sin θ})}^{2} = \frac{m g^{2} cos θ}{2 c {sin}^{2} θ}$
Now, $v = \frac{d S}{d t} = \frac{c cos θ}{2 m} t^{2}$
$t \int 0 t d t or S = (\frac{c cos θ}{6 m}) t^{3}$
So the distance traversed till the time of break off i.e in the time interval $t = \frac{m g}{c sin θ}$ is given by
$S = \frac{c cos θ}{6 m} {(\frac{m g}{c sin θ})}^{3} = \frac{m^{2} g^{2} cos θ}{6 c^{2} {sin}^{3} θ}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
At the moment t=0 force F=kt is applied to a small body of mass m resting on a smooth horizontal plane (k is a constant) The direction of this force always forms an angle $θ$ with the horizontal as shown.

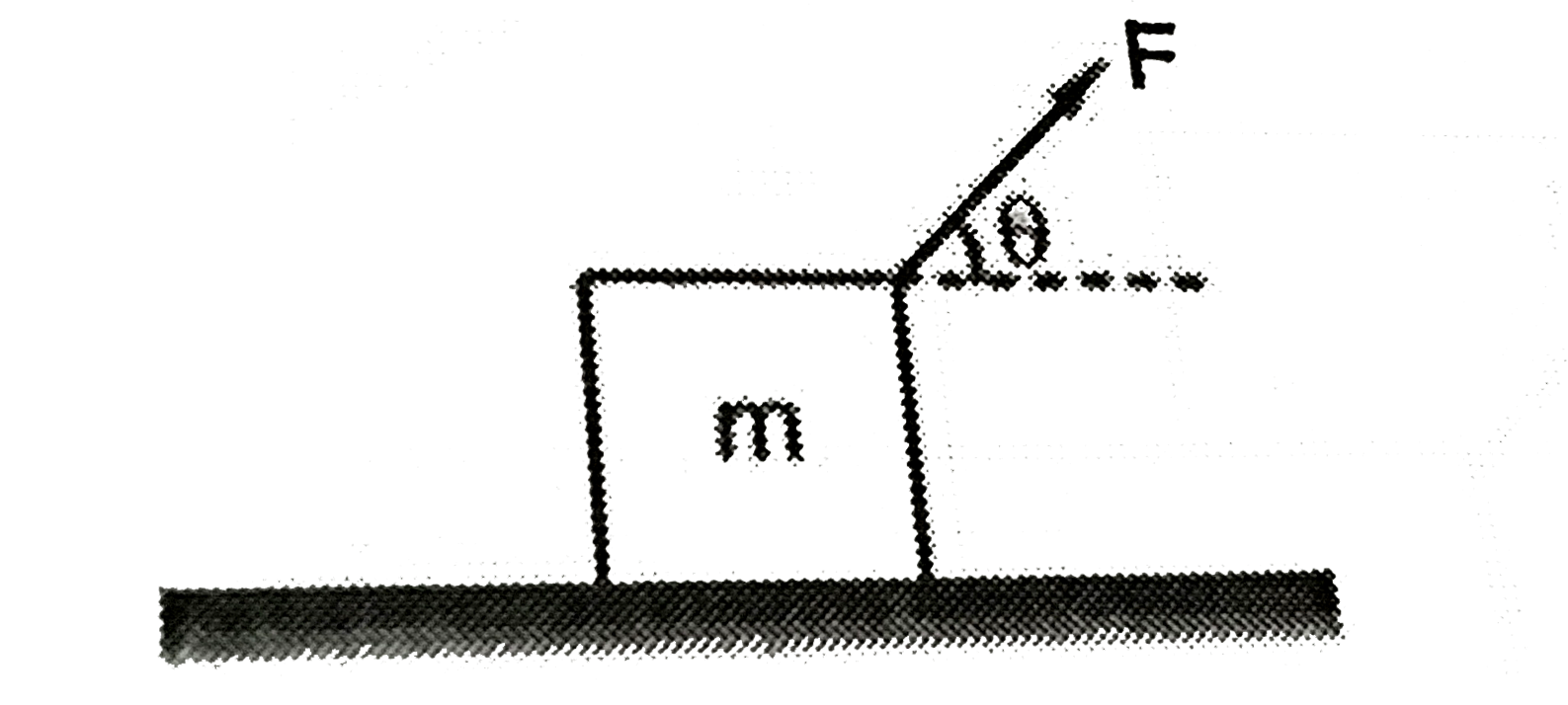
Find the time t at which moment, the body breaks off the plane:
A $\frac{m g}{2 k sin θ}$
B $\frac{m g}{k sin θ}$
C $\frac{m g}{k {sin}^{2} θ}$
D $\frac{2 m g}{k sin θ}$
Question 2 - Select One or More
At $t = 0$ , a force $F = a t^{2}$ is applied to s small body of mass m at an angle $α$ resting on a smooth horizontal plane.

AVelocity of the body at the moment it breaks off the plane is $\sqrt{\frac{m g^{3}}{9 a {tan}^{2} α sin α}}$
BThe distance travelled by the body before breaking off the plane is $\frac{m g^{2}}{12 a sin α tan α}$
CIts acceleration at the time of breaking off the plane is $g cot α$ .
DTime at which it breaks off the plane is $\sqrt{\frac{m g}{a sin α}}$
Question 3 - Select One
Work done by the gravitational force on a body of mass $'' m''$ moving on a smooth horizontal surface through a distance $' s'$ is
A $m g s$
B $- m g s$
C $0$
D $2 m g s$

NARAYNA-NEWTONS LAWS OF MOTION-SINGLE ANSWER QUESTIONS

Home
Ask Doubt
Profile