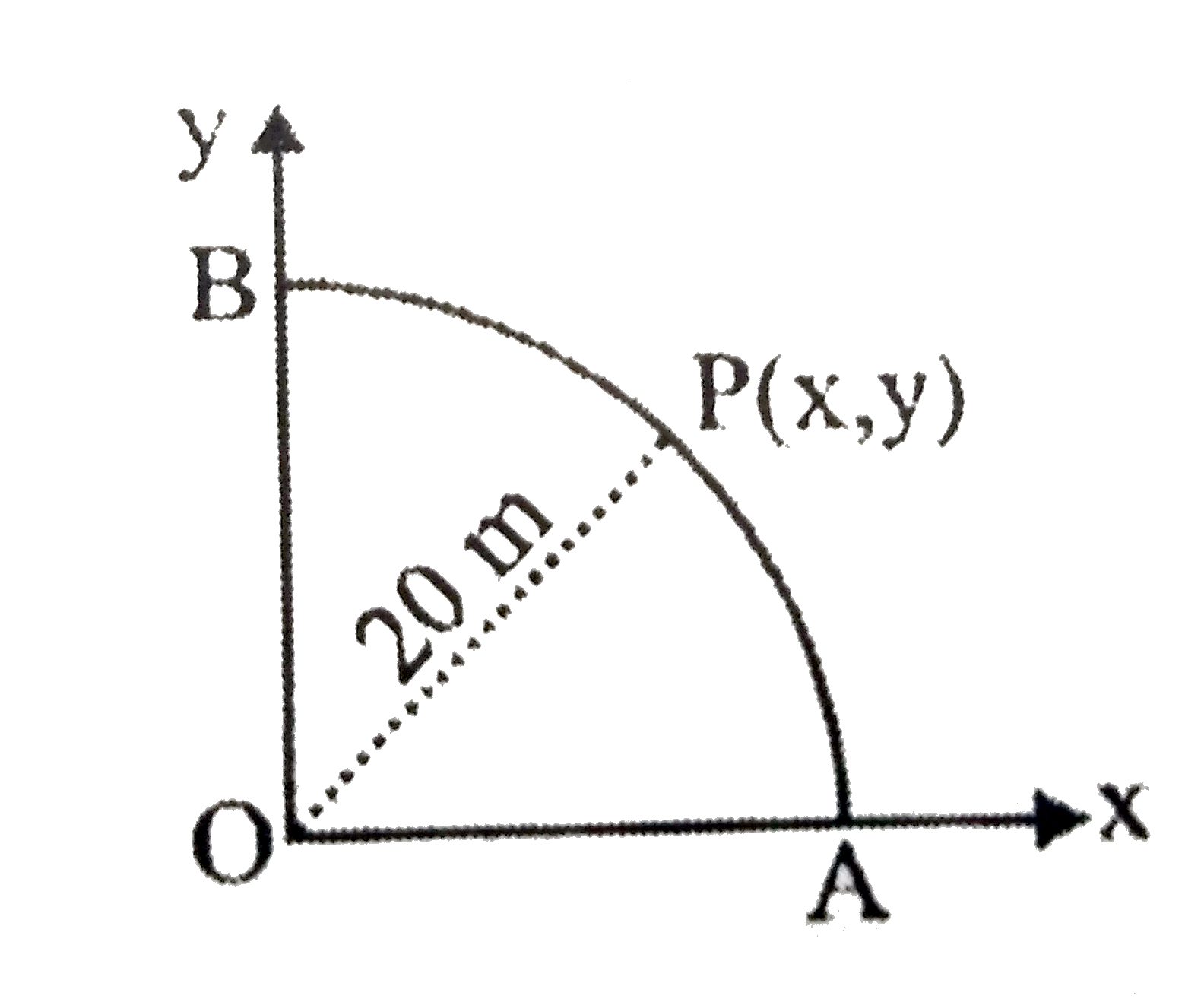
A point P moves in counter-clockwise direction on figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in metre and t is in second. The radius of the pathh is 20 m. the acceleration of P when t=2s is nearly
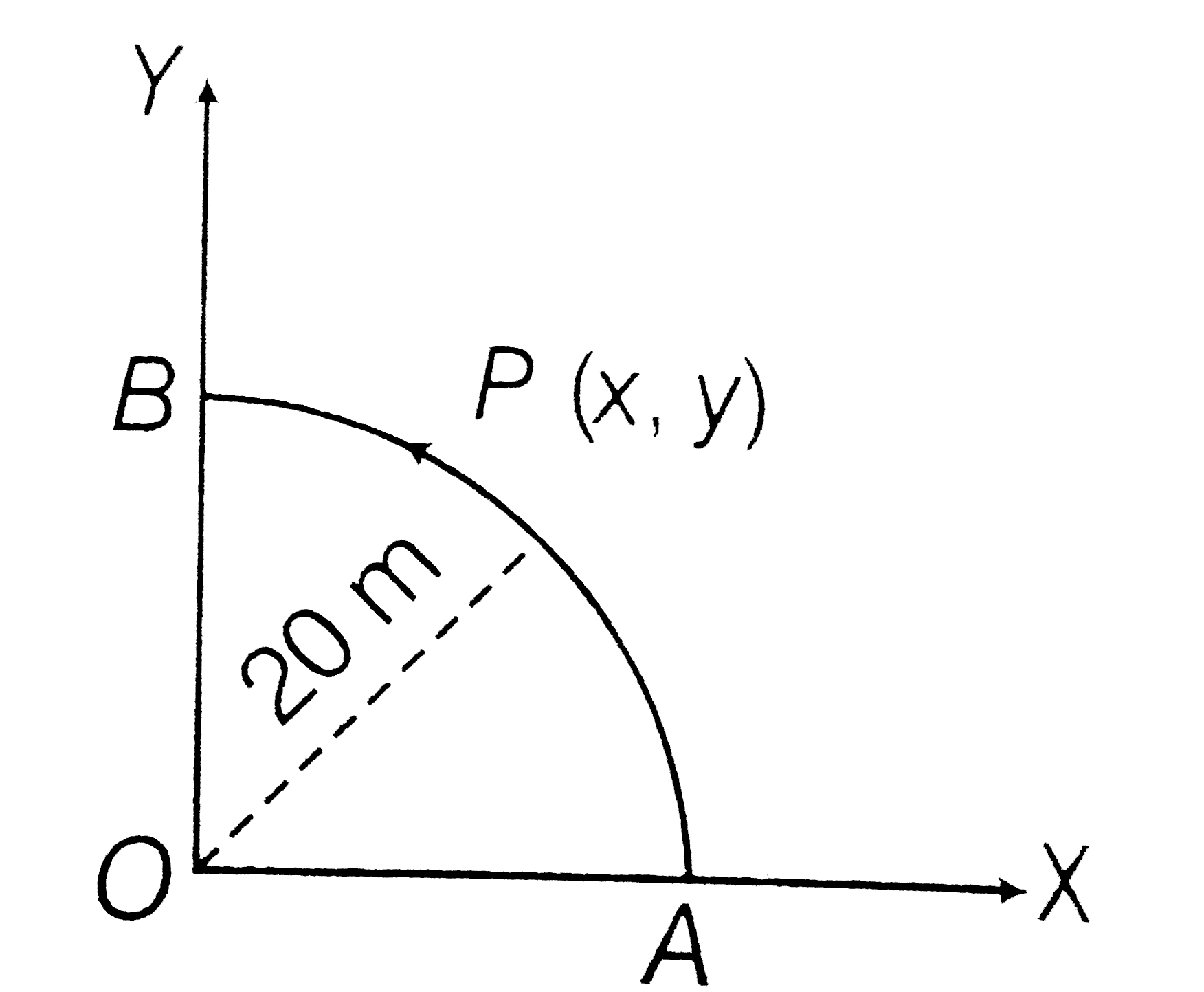
S=t3+5⇒v=dSdt=3t2
For t=2s,v=3×4=12ms−1
Tangential acceleration, at=dvdt=6t
For t=2s,at=12ms−2
Centripetal acceleraton
ac=v2R=14420=7.2ms−2
net acceleration =√a2t+a2c≈14ms−2 .
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - C.U.Q
73 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -I (C.W)
47 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV
41 Videos
Similar Questions
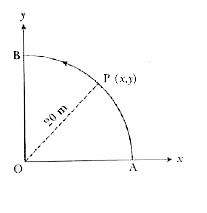
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of P when t = 2 s is nearly
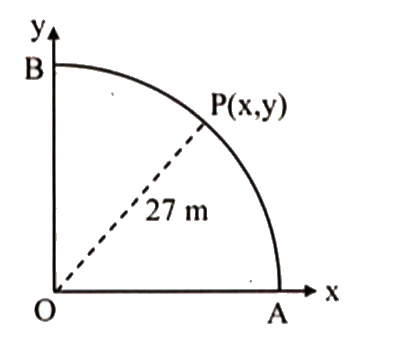
View SolutionA point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5 where s is in the metre and t is in seconds. The radius of the path is 27 m. The acceleration of P when t= 3 s is _________ m/s2. (Take √13=3.6)
View Solution
Knowledge Check
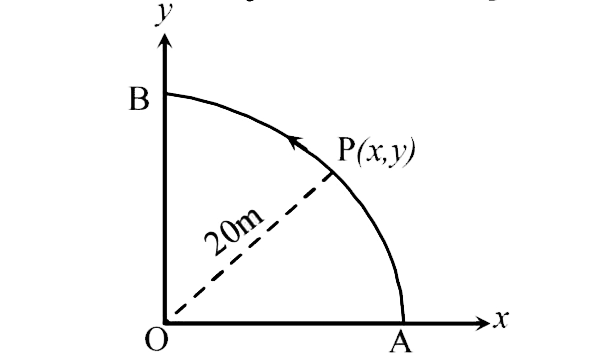
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of P when t = 2 s is nearly
 A14m/s2B13m/s2C12m/s2D7.2m/s2
A14m/s2B13m/s2C12m/s2D7.2m/s2A point p moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length s=t3+5 , where s is in metres and t is in seconds . The radius of the path is 20m . The acceleration of 'P' when t=2s is nearly .
 A13m/s2B12m/s2C7.2m/s2D14m/s2
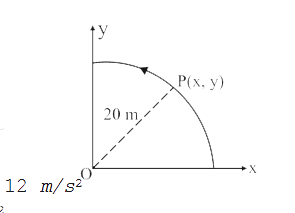
A13m/s2B12m/s2C7.2m/s2D14m/s2A point P moves in counter clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length s=t2+5, wheres is in metres and t is in seconds. The radius of the path is 20m. The acceleration of 'P' when t=5√310 seconds is nearly:
 A2m/s2B1.5m/s2C2.5m/s2D3m/s2
A2m/s2B1.5m/s2C2.5m/s2D3m/s2
A point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5 where s is in the metre and t is in seconds. The radius of the path is 27 m. The acceleration of P when t= 3 s is _________ m/s2. (Take √13=3.6)

View SolutionThe displacement of a particle is represented by the equation, s=3t3=7t2+4t+8 where (s) is in metres and (t) in seconds . The acceleration of the particle at t=1s is.
View SolutionA point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P ' is such that it sweeps out a length s=t3+5 where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of ' P ' when t = 2 s is nearly:
View SolutionThe displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
View SolutionThe displacment of a particle is represented by the following equation : s=3t3+7t2+5t+8
where s is in metre and t in second. The acceleration of the particle at t=1:-
View Solution
