In the previous problem
(i) At θ=cos−1(23), the particle will lwave the hemisphere
(ii) At depth R/3 below A, the particle will leave the hemisphere
(iii) At height 2R/3 above O, the particle will leave the hemisphere
(i),(ii)
(ii),(iii)
(i),(iii)
(i),(ii),(iiii)
The correct Answer is:D
when N=0,i.e.,cosθ=2/3
θ=cos−1(23), the block leaves hemisphere
j=R(1−cosθ)=R3
Topper's Solved these Questions
Similar Questions
A heavy particle of mass m is in motion on a smooth surface of hemisphere of radius R and there is no friction. At the initial instant the particle is at the topmost point A and has an initial velocity v0 At what point will the particle leave the surface of the hemisphere ? Also determine the value of v0 for which the particle will leave the sphere at the initial instant.
View SolutionA particle of mass m slides down from the vertex of semi- hemisphere, without any initial velocity. At what height from horizontal will the particle leave the sphere-
View Solution
Knowledge Check
A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)The volume of a hemisphere is 2.25πcm3. What is the total surface area of the hemisphere?
A2.25πcm2B5πcm2C6.75πcm2D4.5πcm2A skier plans to ski a smooth fixed hemisphere of radius R He starts from rest from a curved smooth surface of height (R/4) the angle θ at which he leaves the hemisphere is
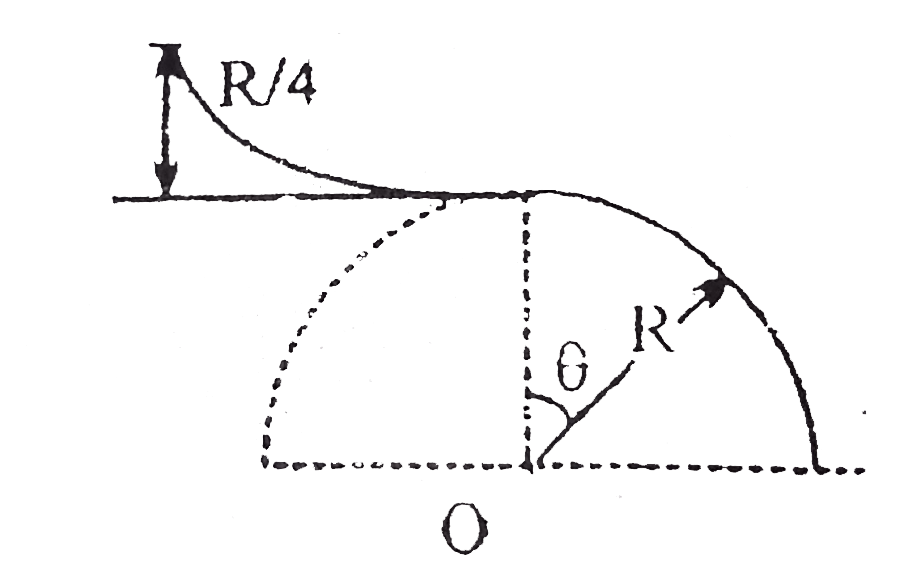 Acos−1(2/3)Bcos−1(5/√3Ccos−1(5/6)Dcos−1(5/2√3
Acos−1(2/3)Bcos−1(5/√3Ccos−1(5/6)Dcos−1(5/2√3
A hemisphere of radius R and of mass 4m is free to Slide with its base on a smooth horizontal table. A particle mass m is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere at an angular displacement θ when velocity of hemisphere has become v.

View SolutionA partcle rests on the top of a hemisphere of radiu R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down it-
View SolutionA partcle rests on the top of a hemisphere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down :
View SolutionA skier plane to ski a smooth fixed hemisphere of radius R . He starts from rest from a curve smooth surface of height (R4) . The angle θ at which he leaves the hemisphere is
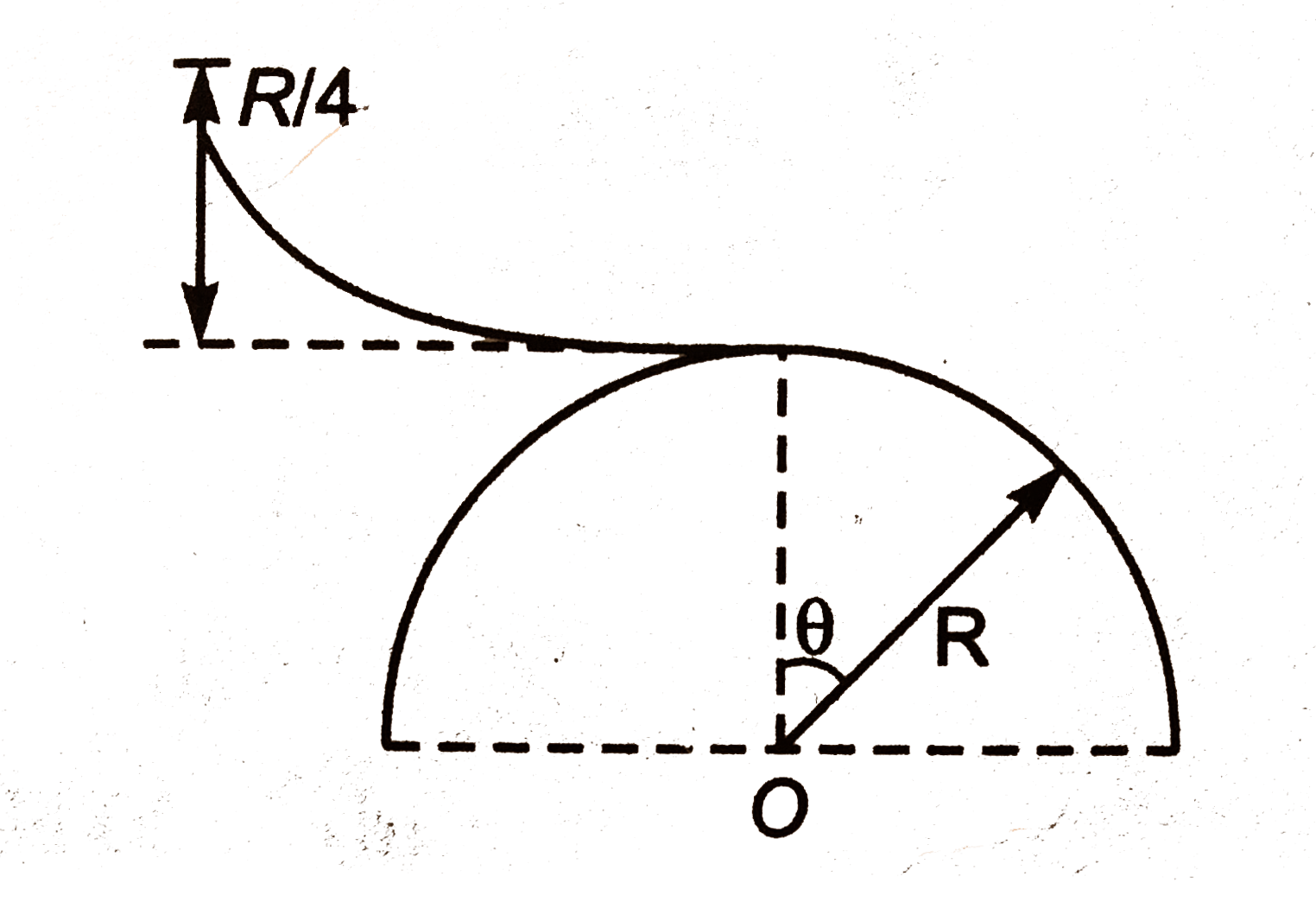
View SolutionA particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
View Solution
