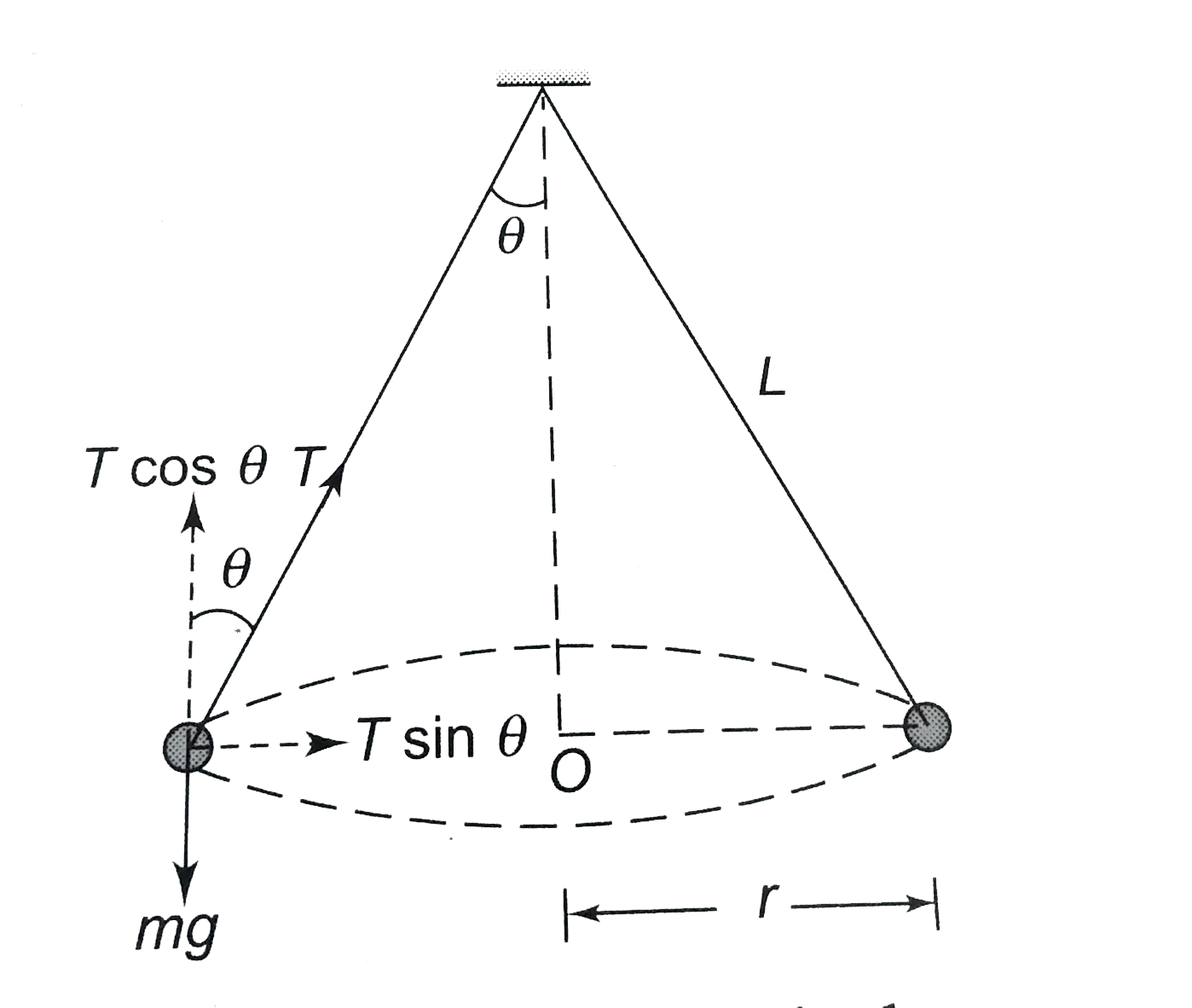
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Sch a system is called a conical pendulum.

Video Solution

Text Solution

Verified by Experts

$θ$ :angle made by the string with vertical
$\sin θ = \frac{r}{L}$
The forces acting on the particle are $(i)$ weight of particle $(m g)$ and $(i i)$ tension in the string.
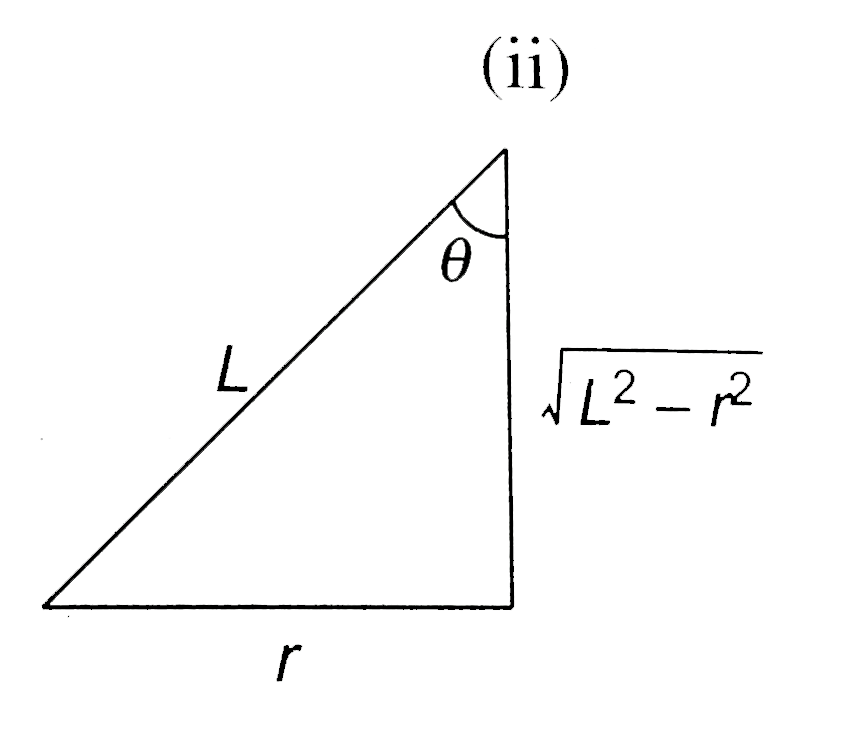
Here, $T \cos θ$ balance the weight and $T \sin θ$ provides neccessary centripetal force. $↑ : T \cos θ = m g$ ... $(i)$
$\to : T \sin θ = \frac{m v^{2}}{r}$ .... $(i i)$
$\tan θ = \frac{v^{2}}{r g} \Rightarrow v = \sqrt{r g \tan θ}$
$T = \frac{m g}{\cos θ}$
$v = \sqrt{r g \tan θ} = {(\frac{r g \times r}{\sqrt{L^{2} - r^{2}}})}^{1 / 2} = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{1} / 4})$
$T = \frac{m g}{\cos θ} = \frac{m g L}{\sqrt{L^{2} - r^{2}}}$

Updated on:21/07/2023

A particle of mass ma is suspended from a ceiling thrugh a string of length $L$ . The prticle moves in a horizontal circle of radius $r$ . Find $(a)$ the speed of the prticle and $(b)$ . the tension in the string. Sch a system is called a conical pendulum
.
A $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
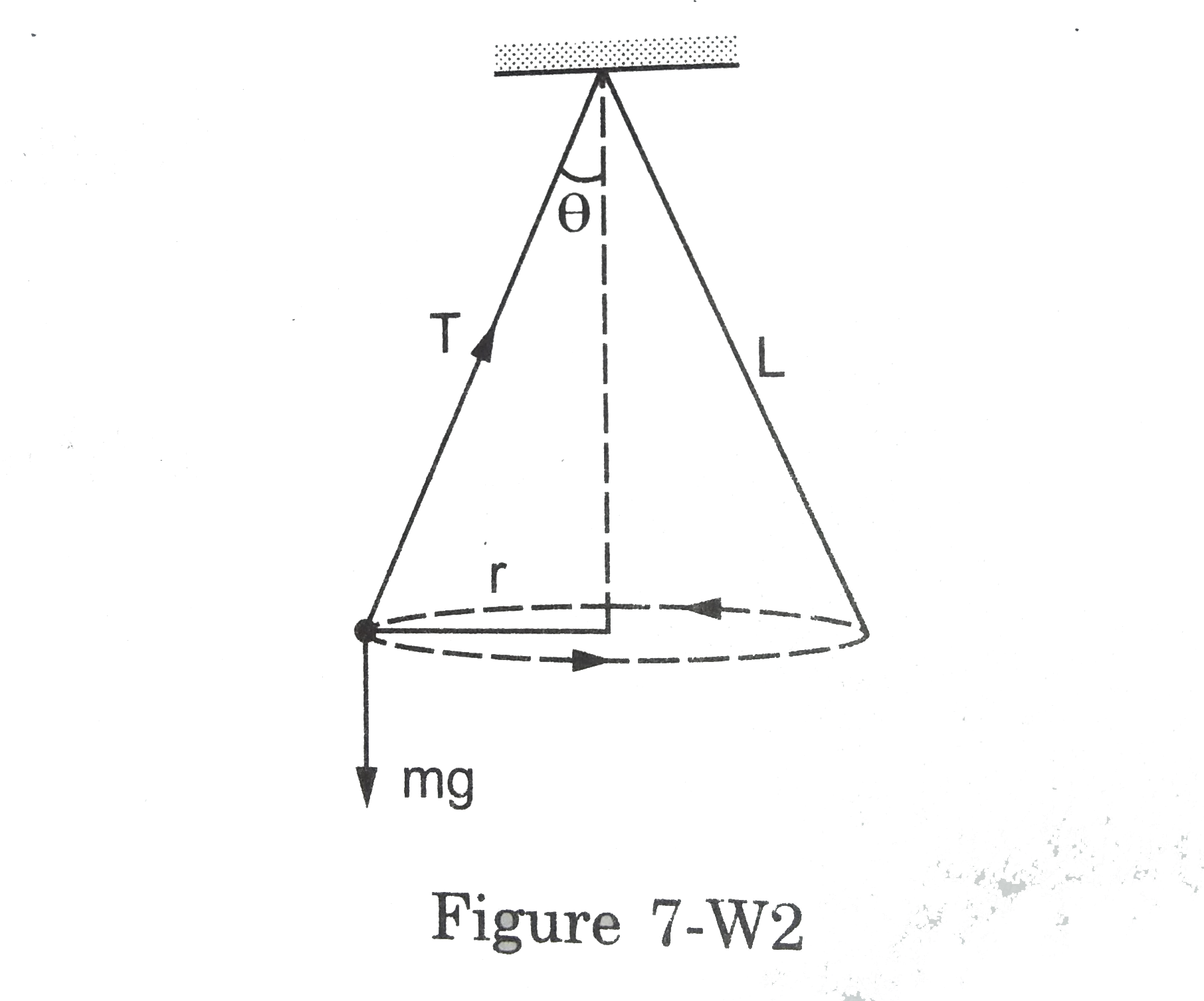
B $v = \frac{r^{2} \sqrt{g}}{{(L^{3} - r^{3})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
C $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L^{2}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
D $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
A $\frac{r g}{\sqrt{L^{2} - r^{2}}}$
B $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$
C $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
D $\frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
A paricle of mass $m$ is tied to a light string of length $L$ and moving in a horizontal circle of radius $r$ with speed $v$ as shown. The forces acting on the particle are

A $m g and T$
B $m g, T, \frac{m v^{2}}{r}$ directed in wards
C $m g, T, \frac{m v^{2}}{r}$ directed outewards
D $\frac{m v^{2}}{r}$ only