Consider the situation as shown. The pulley has a moment of inertia I, and radius r, the block is in equilibrium. Find the time period of mass m. Assume no slipping.

Let at an instant extension of spring is x (after equilibrium), speed of block is v and angular speed of pulley ω.

In equilibrium
mg=kx0,x0: initial extension of spring
The energy of the system
E=12mv2+12Iω2−mgx+12k(x+x0)2
=12mv2+12I(vr)2−mgx+12k(x+x0)2
=12mv2(1+Imr2)−mgx+12k(x+x0)2
Since total energy is constant
dEdt=0
0=12m⋅2vdvdt(1+Imr2)−mg(dxdt)
+12k⋅2(x0+x)dxdt
=mva(1+Imr2)−mgv+kx0v+kxv
=ma+Ir2a+kx
(m+Ir2)a=−kx
a=−(km+I/r2)x=−ω2x
T=2π√m+I/r2k
Topper's Solved these Questions
Similar Questions
Consider the situation as shown in the figure. The pulley has moment of inertia I and radius r. The table is rough and the coefficient of kinetic friction is μk. The system is released from the rest. Calculated speed of block of mass 3m as a function of the distance h it has descended. Assume no slipping.

View SolutionConsider the situation as shown in the diagram. The pulley has radius R and moment of inertia I. The block is release when the spring (spring constant k) is unstretched. Find the speed of block when the vlock has fallen a distance h. Assume no slipping.

View Solution
Knowledge Check
Find the time period of SHM of the block of mass M
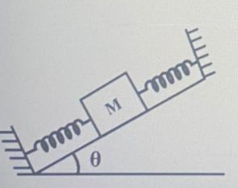 AT=2π√M2KBT=2π√MKCT=2π√2MKDT=2π√M4K
AT=2π√M2KBT=2π√MKCT=2π√2MKDT=2π√M4K
Consider the situation as shown in the figure. The moment of inertia of wheel is 2kgm2 and its radius is 0.25m. Find the angular acceleration of the wheel, assuming no slipping.

View SolutionAn object of mass m is tied to a light string wound around a pulley that has a moment of inertia I and radius R. The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionThe string, spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionFigure shows two blocks of masses m and M connected bky a string pasing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotte about this axis. Find the accelerationof the mass M asuming that the string does not slip on the pulley.
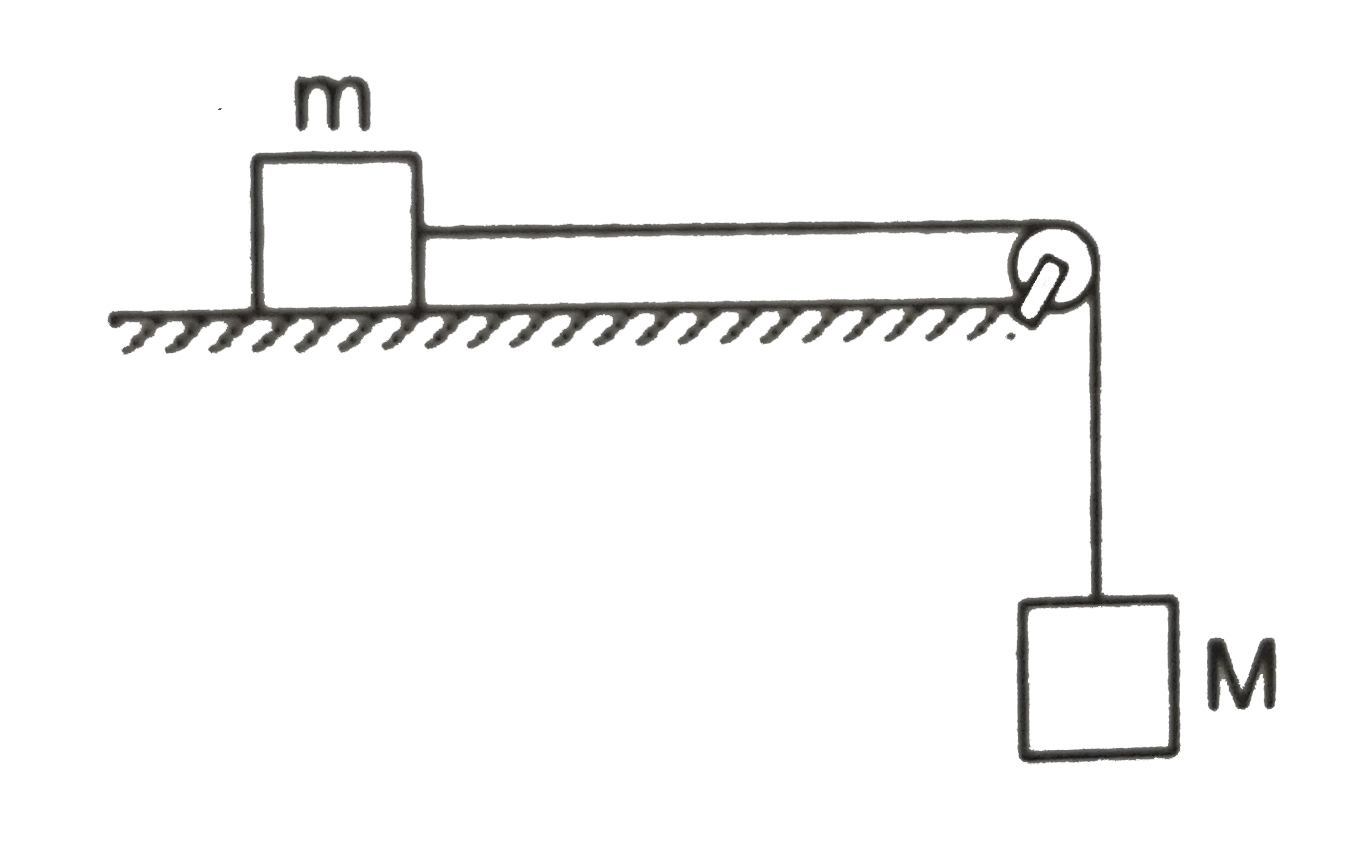
View SolutionSolve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
View SolutionThe string, the spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View Solution
