A particle executes $S H M x = A sin (ω t + ϕ)$ . At $t = 0$ , the position of the particle is $x = \frac{\sqrt{3} A}{2}$ and it moves along the positive x-direction. Find
(a) phase constant $ϕ$
(b) velocity at $t = \frac{π}{ω}$
(c) acceleration at $t = \frac{π}{ω}$

Video Solution

Text Solution

Verified by Experts

$x = A sin (ω t + ϕ)$
At $t = 0, x = \frac{\sqrt{3} A}{2}$
$\sqrt{3} \frac{A}{2} = A sin (ω \times 0 + ϕ) \Rightarrow sin ϕ = \frac{\sqrt{3}}{2}$
$= {sin 60}^{\circ}$ or $120^{\circ}$
$ϕ = 60^{\circ}$ or $120^{\circ}$
$v = \frac{d x}{d t} = A ω cos (ω t + ϕ)$
At $t = 0, v = A ω cos ϕ$
${cos 60}^{\circ} = \frac{1}{2}$ and ${cos 120}^{\circ} = - \frac{1}{2}$
As v is $+ v e$ at $t = 0$ , $ϕ = 60^{\circ} = \frac{π}{3}$
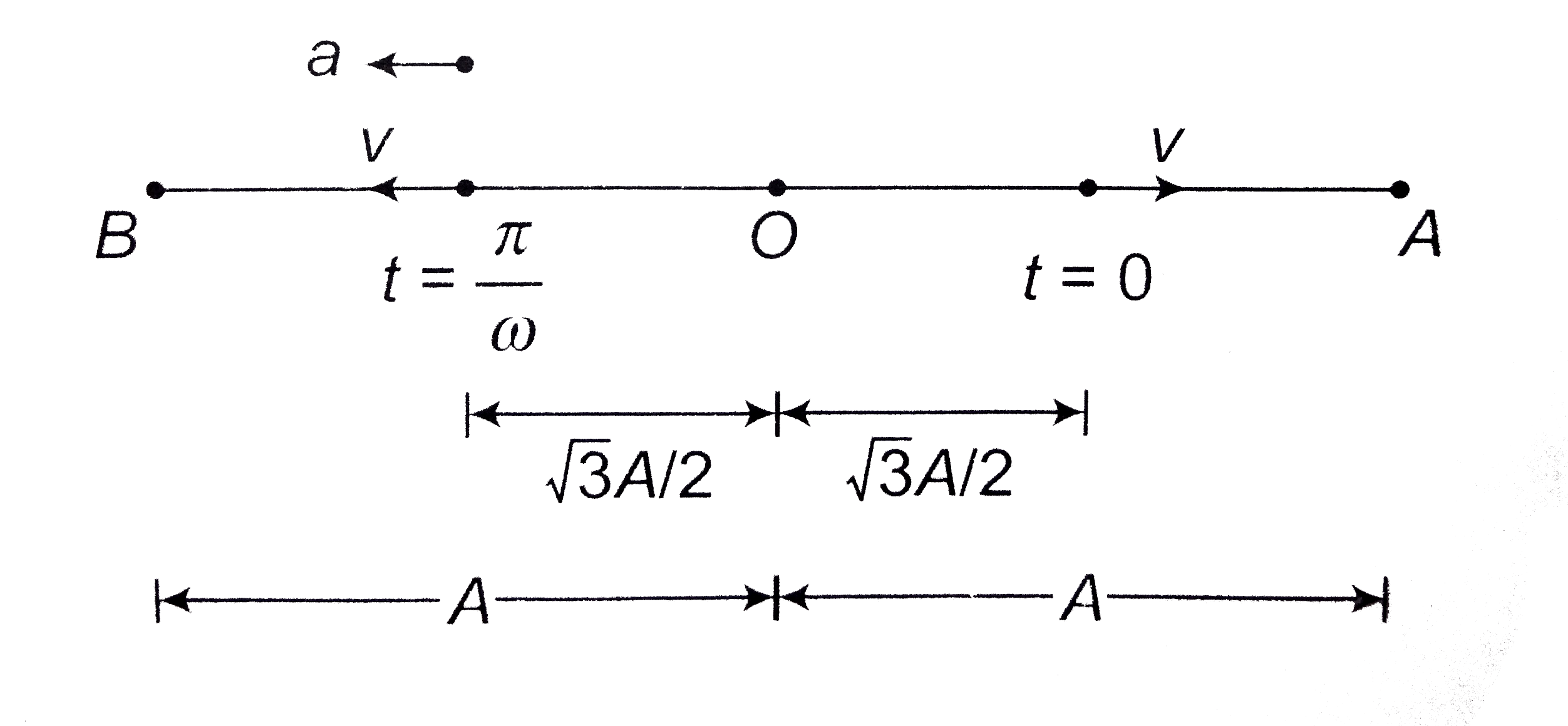
(b) Now $x = A sin (ω t + π / 3)$
$v = A ω cos (ω t + π / 3)$
At $t = π / ω$ , $x = A sin (ω \cdot π / ω + π / 3)$
$= - A \frac{sin π}{3} = \frac{- \sqrt{3} A}{2}$
$v = A ω cos (ω \cdot \frac{π}{3} + \frac{π}{3}) = - A ω cos π / 3 = - \frac{A ω}{2}$
(c) $a = - ω^{2} x$
At $t = \frac{π}{ω}, x = \frac{- \sqrt{3} A}{2}$
$a = - ω^{2} (- \frac{\sqrt{3} A}{2}) = \frac{\sqrt{3} ω^{2} A}{2}$

Updated on:21/07/2023

The displacement-time equation of a particle executing SHM is $A - A sin (ω t + ϕ)$ . At tme t=0 position of the particle is x= $\frac{A}{2}$ and it is moving along negative x-direction. Then the angle $ϕ$ can be
A $\frac{π}{6}$
B $\frac{π}{3}$
C $\frac{2 π}{3}$
D $\frac{5 π}{6}$
The displecemen-time equation of a particle execitting $S H M$ is $x = A sin (ω t + ϕ)$ At time $t = 0$ position of are position is $x = A / 2$ and it is moving along negative $x - d i r e c t i o n$ .Then the angle $ϕ$ can be
A ${[\frac{1}{k_{1}} + \frac{1}{k_{2}}]}^{1}$
B $(4 t - \frac{π}{6})$
C $\frac{1}{2 π} {(\frac{k_{1} + k_{2}}{M})}^{1 / 2}$
D $\frac{1}{2 π} {(\frac{k_{1} - k_{2}}{M})}^{1 / 2}$
A particle is executing SHM, whose equation is given below
$x = A cos (ω t + ϕ)$ . If t=0 , particle is mean position going towards positive x-direction then $ϕ$ is equal to
A0
B $π / 2$
C $π$
Dnoone of the above