A1though quantum mechanics tells us that we cannot pinpoint an electorn in an atom, it does define the region where the electron might be at a given time. The concept of_______gives the probability that an electron will be found in a particular region of an atom.
electron mass
electron charge
electron size
electron density
The correct Answer is:D
The square of the waves function (ψ2) denfines the distribution of electron density in space around the nucleus.
Topper's Solved these Questions
- STRUCTURE OF ATOMBOOK - R SHARMACHAPTER - STRUCTURE OF ATOMEXERCISE - Follow-up Test 2
1 Videos
- STRUCTURE OF ATOMBOOK - R SHARMACHAPTER - STRUCTURE OF ATOMEXERCISE - Follow-up Test 3
1 Videos
- STRUCTURE OF ATOMBOOK - R SHARMACHAPTER - STRUCTURE OF ATOMEXERCISE - Follow-up Test 1
1 Videos
- STATES OF MATTERBOOK - R SHARMACHAPTER - STATES OF MATTEREXERCISE - ARCHIVES
41 Videos
- THE P BLOCK ELEMENTSBOOK - R SHARMACHAPTER - THE P BLOCK ELEMENTSEXERCISE - Archives
40 Videos
Similar Questions
A: Bohr's orbits are regions where the electron may be found with large probability.
R: The orbital picture in Bohr's model of the hydrogen atom was inconsistent with the uncertainty principle.
View SolutionAn electron in an atom can be completely designated with the help of four quantum numbers. Out of these, the first three i.e., principal (n), azimuthal (l) and magnetic (m) quantum number are obtained from the solution of Shrodinger wave equation while the spin(s) quantum number arises from the spin of the electron around its axis clockwise or antiaclockwise. Ot of these principal quantum number tells about the size, azimuthal quantum number about the shape and magnetic quantum signifies the orientation of the electron orbital.
How many electrons in a given atom have the following set of quantium numbers?
n=3,l=2,m=+2,s=−1/2
View Solution
Knowledge Check
After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
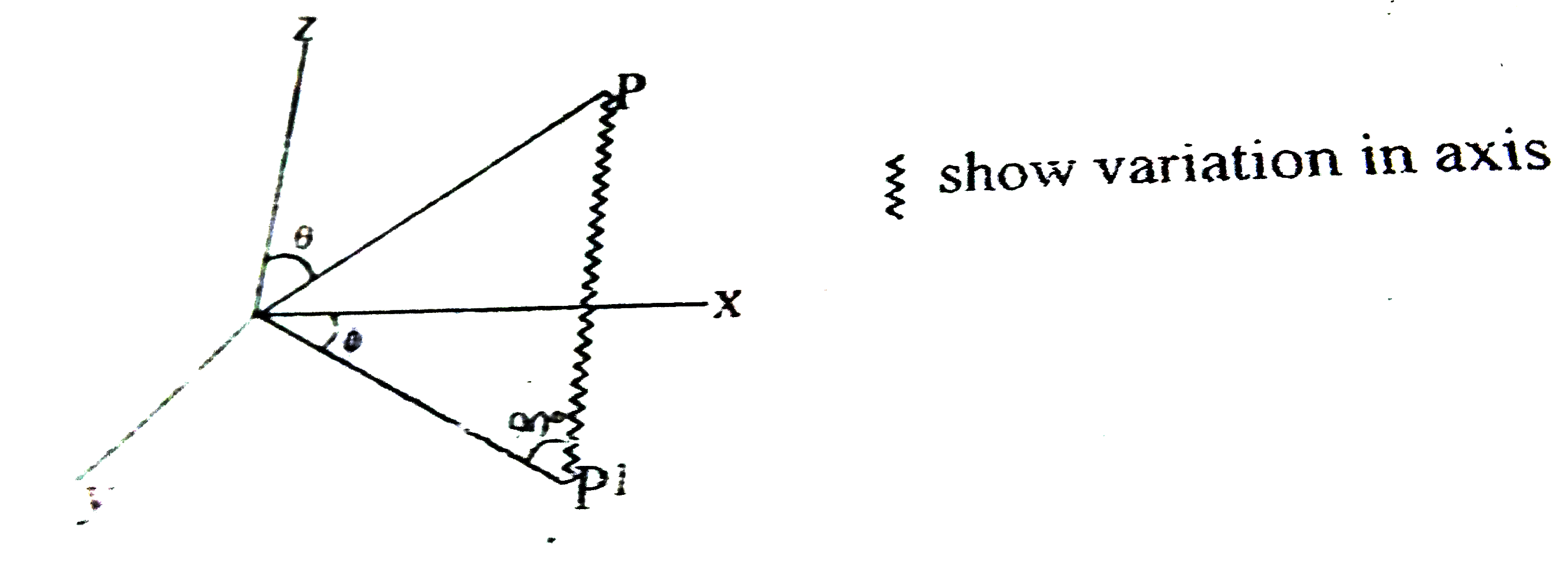
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle onlyA1s and 2sB2pz and 2d2zC2px and 3d2zD2px and 2sAfter the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
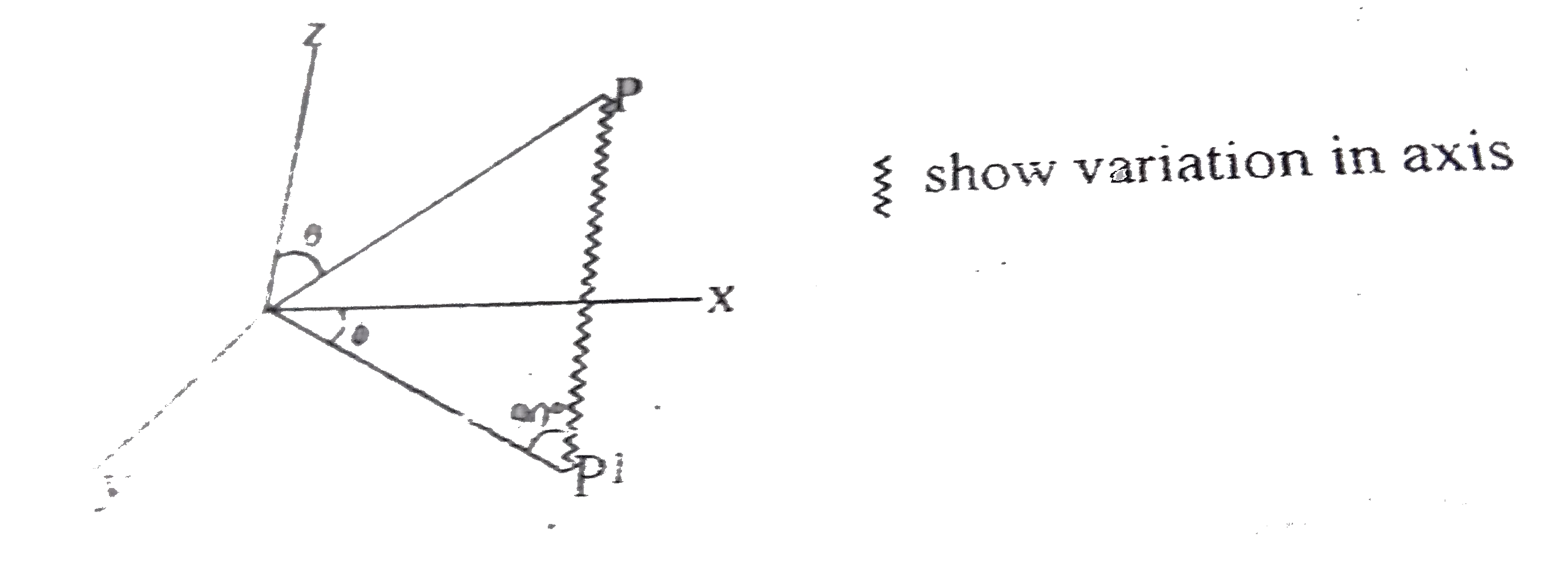
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The electron probility density for 1s-orbital best represented by the relation.A12√π(Za0)3/2×era0B1π(Za0)3×e−2zra0C1π(Za0)3/2×era0D2π(Za0)3×e−2zra0A region in space around the nucleus of an atom where the probability of finding the electron is maximum is called
Asub-levelBorbitCorbitalDelectron shell
Orbital is the region in an atom where the probability of finding the electron around the nucleus. Orbitals do not specify a definite path according to the uncertainty principle. An orbital is described with the help of wave function Φ. Whenever an electron is described by a wave function, we say that an electron occupies that orbital. Since, many wave functions are possible for an electron, there are many atomic orbitals in an atom. Orbitals have different shapes, except s-orbitals, all other orbitals hae different shapes, except s-orbitals, all other orbital have different shapes, except s-orbitals, all other orbitals have directional character. Number of spherical nodes in an orbital is equal to (n−l−1). Orbital angular momentum of an electron is √l(l+1)h.
Q. When an atom is placed in a magnetic field, the possible number of orientations for an orbital of azimuthal quantum number 3 is:
View SolutionAn atom is assumed to tbe spherical in shape and thus, the size of atom is generally given in terms of radius of the sphere and is called atomic radius. It is usually defined as the distance between the centre of the nucleus and outermost shell where electron are present. The exact measure of atomic radius is not easy due to following reasons:
(i) The atom does not have well defined boundary. the probability of finding the electron is never zero even at large distance from the nucleus.
(ii) It is not possible to get an isolated atom. the electron density around an atom is affected by the presence of neighbouring atoms, i.e., the size of the atom changes in going from one set of environement to another.
(iii) the size of an atom is very small, of the order of about 1.2 Å,i.e., 1.2×10−10m.
An estimate of the size of the atom can, however, be made by knowing the distance betweent he atoms in the combined state. the distance between the atoms, i.e., bond length are generally measured by the application of techniques such as X-ray differaction, electron diffraction, infrared spectroscopy, nuclear magnetic resonance spectroscopy, etc. However, bond lengths change with different type of bonding. Three types of radius are commonly used, i.e.,
(a) Covalent radius (b) crystals radius (c) Vander waal's radius
Choose incorrect option regarding atomic radius
View SolutionAn atom is assumed to tbe spherical in shape and thus, the size of atom is generally given in terms of radius of the sphere and is called atomic radius. It is usually defined as the distance between the centre of the nucleus and outermost shell where electron are present. The exact measure of atomic radius is not easy due to following reasons:
(i) The atom does not have well defined boundary. the probability of finding the electron is never zero even at large distance from the nucleus.
(ii) It is not possible to get an isolated atom. the electron density around an atom is affected by the presence of neighbouring atoms, i.e., the size of the atom changes in going from one set of environement to another.
(iii) the size of an atom is very small, of the order of about 1.2 Å,i.e., 1.2×10−10m.
An estimate of the size of the atom can, however, be made by knowing the distance betweent he atoms in the combined state. the distance between the atoms, i.e., bond length are generally measured by the application of techniques such as X-ray differaction, electron diffraction, infrared spectroscopy, nuclear magnetic resonance spectroscopy, etc. However, bond lengths change with different type of bonding. Three types of radius are commonly used, i.e.,
(a) Covalent radius (b) crystals radius (c) Vander waal's radius
Choose incorrect option regarding atomic size
View SolutionAn atom is assumed to tbe spherical in shape and thus, the size of atom is generally given in terms of radius of the sphere and is called atomic radius. It is usually defined as the distance between the centre of the nucleus and outermost shell where electron are present. The exact measure of atomic radius is not easy due to following reasons:
(i) The atom does not have well defined boundary. the probability of finding the electron is never zero even at large distance from the nucleus.
(ii) It is not possible to get an isolated atom. the electron density around an atom is affected by the presence of neighbouring atoms, i.e., the size of the atom changes in going from one set of environement to another.
(iii) the size of an atom is very small, of the order of about 1.2 Å,i.e., 1.2×10−10m.
An estimate of the size of the atom can, however, be made by knowing the distance betweent he atoms in the combined state. the distance between the atoms, i.e., bond length are generally measured by the application of techniques such as X-ray differaction, electron diffraction, infrared spectroscopy, nuclear magnetic resonance spectroscopy, etc. However, bond lengths change with different type of bonding. Three types of radius are commonly used, i.e.,
(a) Covalent radius (b) crystals radius (c) Vander waal's radius
The correct order of effective nuclear charge Zeff is
View SolutionOrbital is the region in an atom where the probability of finding the electron around the nucleus. Orbitals do not specify a definite path according to the uncertainty principle. An orbital is described with the help of wave function Φ. Whenever an electron is described by a wave function, we say that an electron occupies that orbital. Since, many wave functions are possible for an electron, there are many atomic orbitals in an atom. Orbitals have different shapes, except s-orbitals, all other orbitals hae different shapes, except s-orbitals, all other orbital have different shapes, except s-orbitals, all other orbitals have directional character. Number of spherical nodes in an orbital is equal to (n−l−1). Orbital angular momentum of an electron is √l(l+1)h.
Q. Orbital angular momentum of f-electrons is:
View Solution
