ifA={(x,y):y=4x,x≠0}and
B={(x,y):x2+y2=8,x,y∈R},then
A∩B=ϕ
A∩B contains one point only
A∩Bcontains two points only
A∩B is a multiple of 4 points only .
The correct Answer is:C
To find the intersection of the sets A and B, we need to solve the equations that define these sets.
1. Define the sets:
- Set A={(x,y):y=4x,x≠0}
- Set B={(x,y):x2+y2=8,x,y∈R}
2. Substitute the equation of set A into the equation of set B:
- Since y=4x, substitute this into the equation of set B:
x2+(4x)2=8
3. Simplify the equation:
- This becomes:
x2+16x2=8
4. Multiply through by x2 to eliminate the fraction (note that x≠0):
x4−8x2+16=0
5. Let z=x2 (this substitution simplifies the equation):
- The equation now becomes:
z2−8z+16=0
6. Factor the quadratic equation:
- This can be factored as:
(z−4)2=0
- Thus, z=4.
7. Solve for x:
- Since z=x2, we have:
x2=4⟹x=2 or x=−2
8. Find corresponding y values:
- For x=2:
y=42=2
- For x=−2:
y=4−2=−2
9. List the intersection points:
- The points in the intersection A∩B are:
(2,2) and (−2,−2)
10. Conclusion:
- Therefore, the number of elements in the intersection A∩B is 2.
- Set A={(x,y):y=4x,x≠0}
- Set B={(x,y):x2+y2=8,x,y∈R}
- Since y=4x, substitute this into the equation of set B:
x2+(4x)2=8
- This becomes:
x2+16x2=8
x4−8x2+16=0
- The equation now becomes:
z2−8z+16=0
- This can be factored as:
(z−4)2=0
- Thus, z=4.
- Since z=x2, we have:
x2=4⟹x=2 or x=−2
- For x=2:
y=42=2
- For x=−2:
y=4−2=−2
- The points in the intersection A∩B are:
(2,2) and (−2,−2)
- Therefore, the number of elements in the intersection A∩B is 2.
Topper's Solved these Questions
- SETSBook:OBJECTIVE RD SHARMAChapter:SETSExercise:Chapter Test
Explore 30 Videos
- SETSBook:OBJECTIVE RD SHARMAChapter:SETSExercise:Section I - Solved Mcqs
Explore 24 Videos
- SEQUENCES AND SERIESBook:OBJECTIVE RD SHARMAChapter:SEQUENCES AND SERIESExercise:Chapter Test
Explore 60 Videos
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:Chapter Test
Explore 34 Videos
Similar Questions
Knowledge Check
ifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):x2+y2=9,x,y∈R},thenAA−B=ϕBB−A=BCA∩B≠ϕDA∩B=AIF sets A and B are defined as A={(x,y):y−1x,0≠x∈R}
B={(x,y):y=−x,x∈R},thenAA∩B=ABA∩B=BCA∩B=ϕDnone of theseIf sets A and B defines as A={(x,y),y=1x,0≠x∈R} and B={(x,y)}:y=-x, x∈R then
AA∩B=ABA∩B=BCA∩B=ϕDNone of the above
In some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
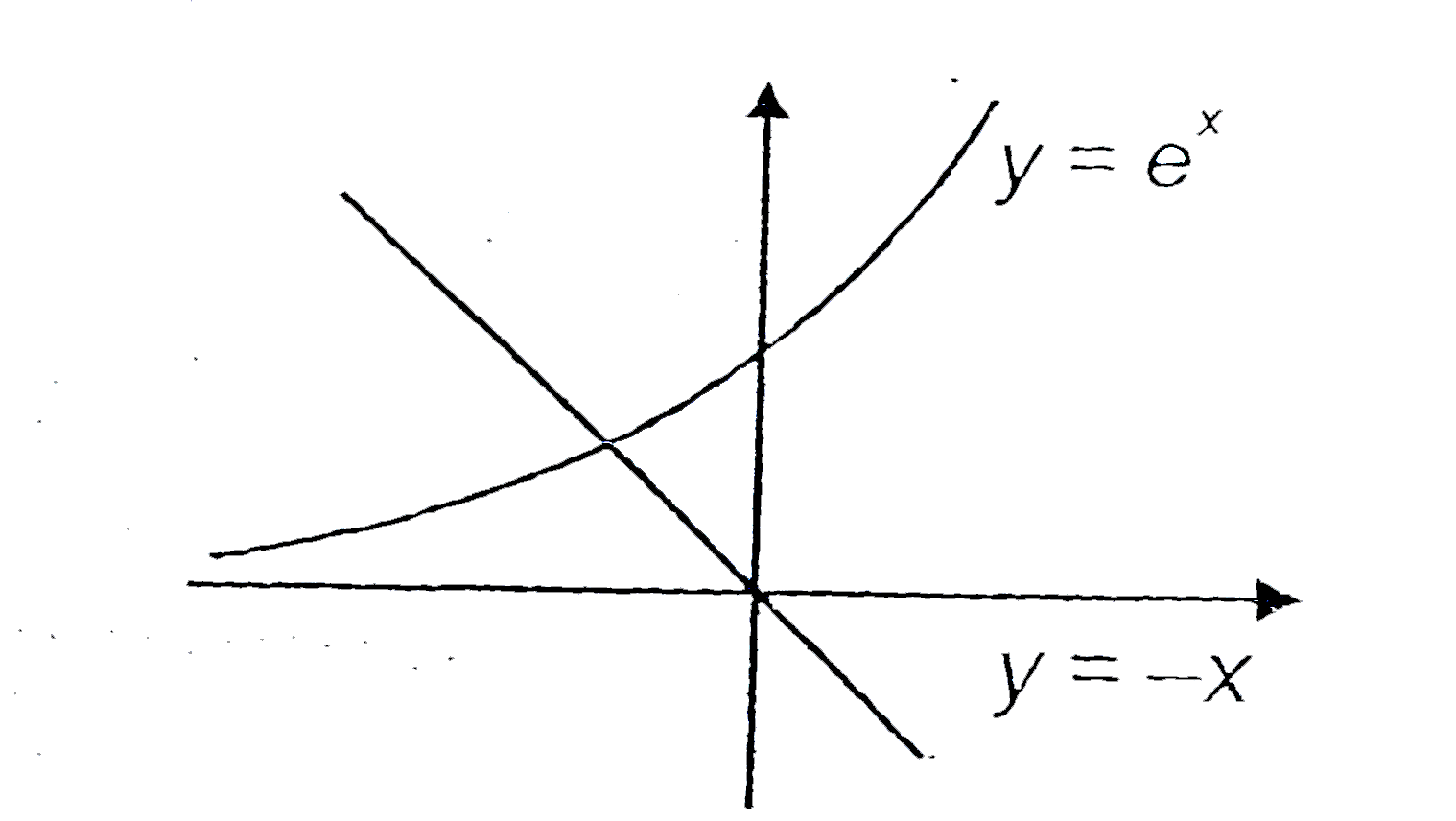
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):Y=|x|,x,y∈R} then
View SolutionIf A={(x,y):x2+y2≤1:x,y∈R} and B={(x,y):x2+y2≥4,x,y∈R}, then
View SolutionIf A={(x,y):x2+y2≤1:x,y∈R} and B={(x,y):x2+y2≥4,x,y∈R}, then
View SolutionifA={(x,y):x2+y2≤1,x,y∈R]and
B={(x,y):x2+y2≤x2+y2≤4,x,y∈R]then
View Solution

