Consider a frictionless ramp on which a smooth object is made to side down from an initial height 'h'. The distance 'd' necessary to stop the object on a flat track ( or coefficient of friction 'μ'), kept at the ramp end is
h/μ
μh
μ2h
h2h
The correct Answer is:A
Step by step video, text & image solution for Consider a frictionless ramp on which a smooth object is made to side down from an initial height 'h'. The distance 'd' necessary to stop the object on a flat track ( or coefficient of friction 'mu'), kept at the ramp end is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)
21 Videos
- FRICTION IS SOLIDS AND LIQUIDS BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (CRITICAL THINKING)
68 Videos
- FORCE BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Evaluation Test
16 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - TARGET PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - Evaluation Test
12 Videos
Similar Questions
In the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
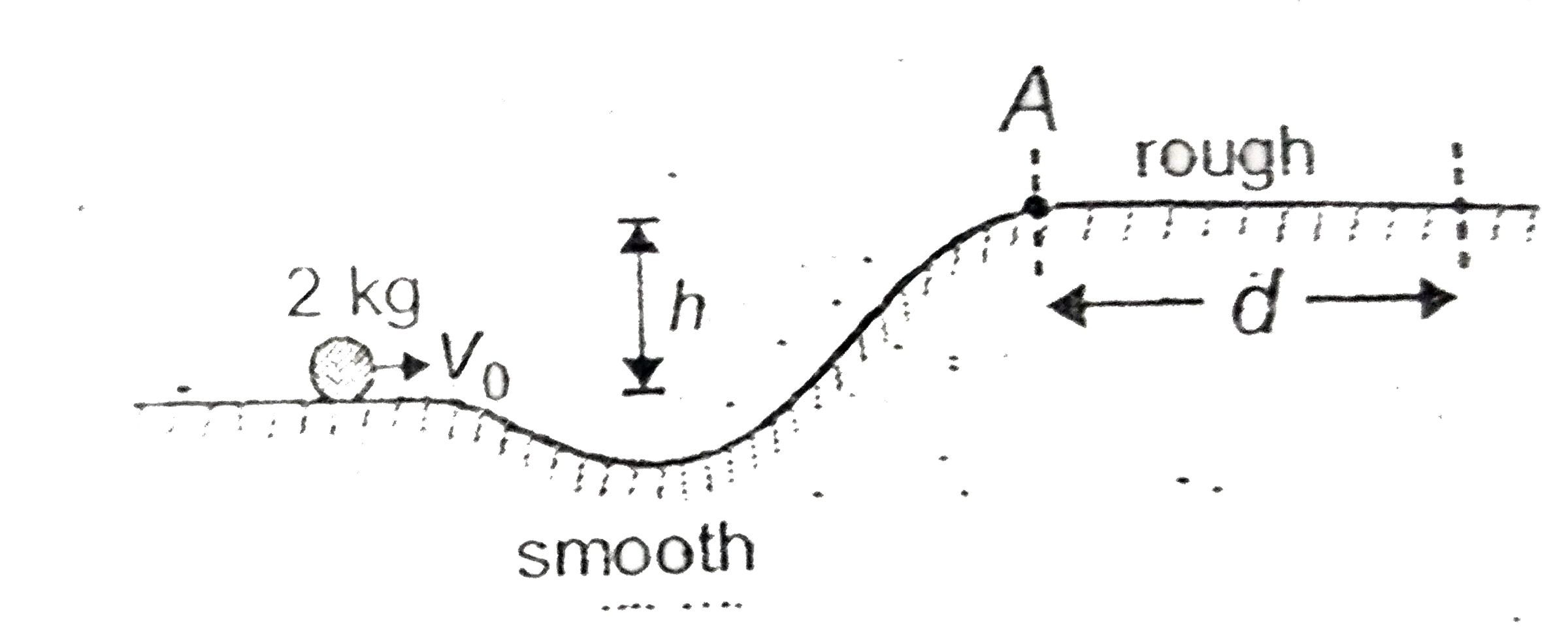
The speed of body at the higher level A is
View SolutionIn the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
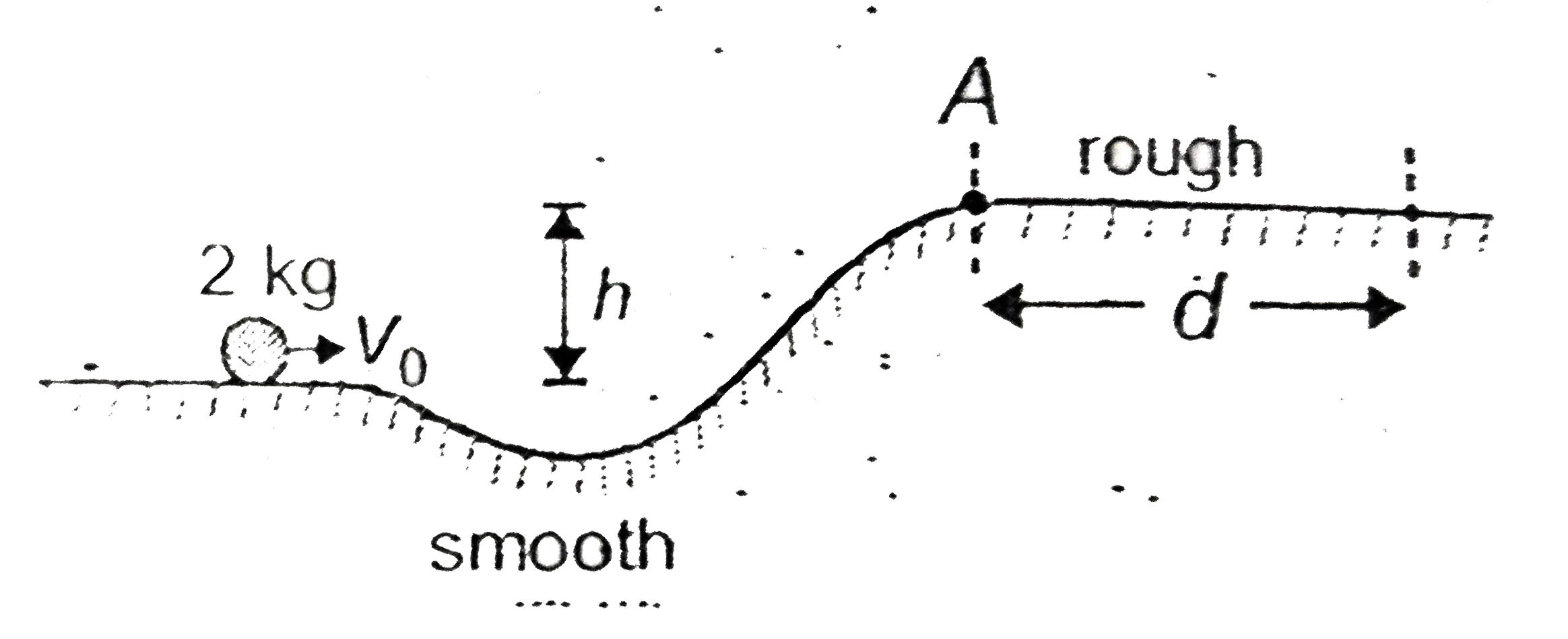
What is the work done by friction force on the body during the motion.
View Solution
Knowledge Check
An object is placed on the surface of a smooth inclined plane of inclination θ. It takes time t to reach the bottom. If the same object is allowed to slide down a rough inclined plane of inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by:-
Aμ=tanθ(1−1n2)Bμ=cotθ(1−1n2)Cμ=tanθ√1−1n2Dμ=cotθ√1−1n2A small object is kept on a groove on rough incline plane of inclination θ. Groove wakes an angle α as shown in diagram. μ coefficient of friction. Which of the following is correct
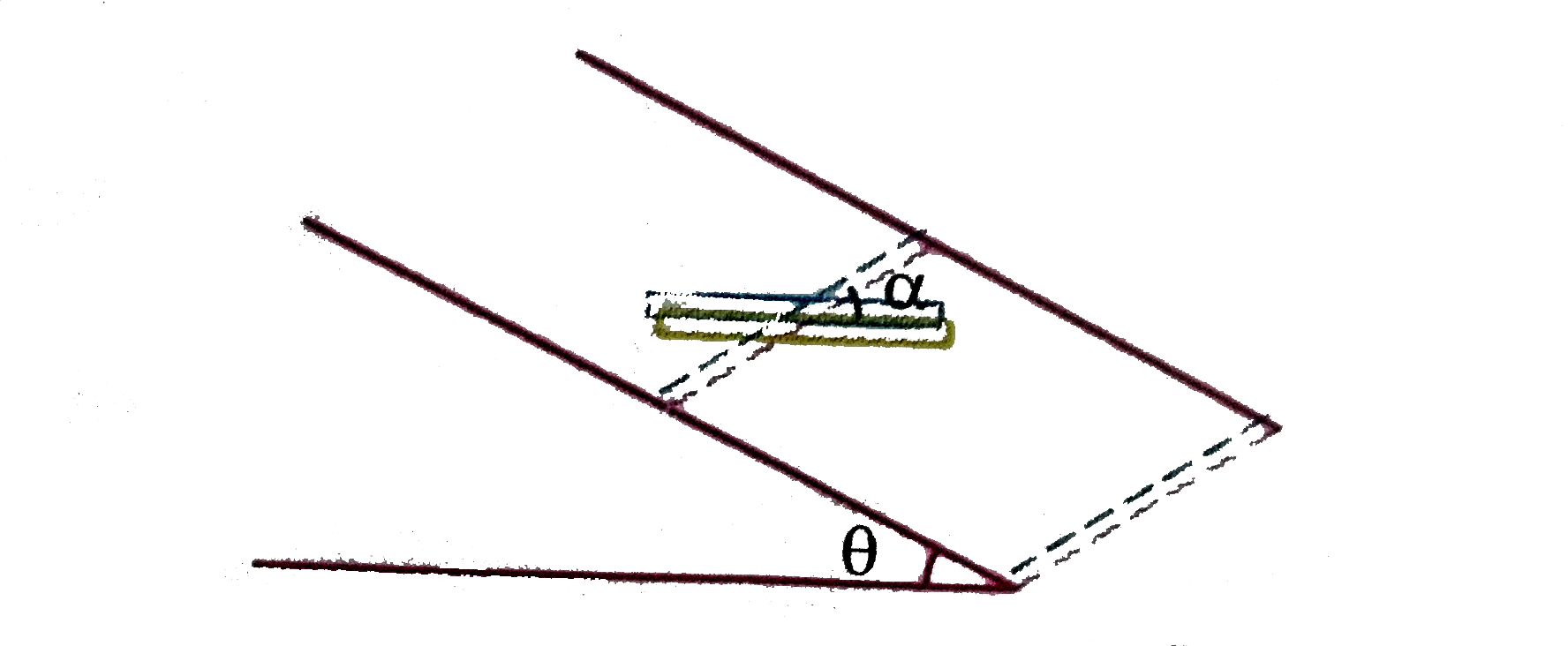 ANormal force by incline plane. N=mgcosθBNormal force by incline is N=mg√cos2θ+sin2θsin2αCmaximum frictional force that can develop is fmax=μmgcosθDIf μ=0 then acceleration of blocks is gsinθcosα
ANormal force by incline plane. N=mgcosθBNormal force by incline is N=mg√cos2θ+sin2θsin2αCmaximum frictional force that can develop is fmax=μmgcosθDIf μ=0 then acceleration of blocks is gsinθcosαA block of mass m is kept on a smooth surface. It is also in contact with a thin plank of mass M=2m, one end of which is clamped to a wall as shown in the figure. The length of the plank is L. The block is given an initial velocity v0, towards right and initially the block is at a distance x0 from hinge. Coefficient of friction between the plank and block is μ.
Assume that througout the motion block remains, below the rod, then at what position from the fixed point it will stop?
(GIven β=v202μgL)
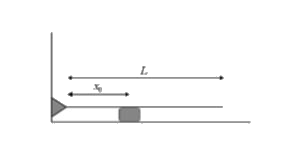 Ax0e2βBx0eβCx0e−2βDx0e−β
Ax0e2βBx0eβCx0e−2βDx0e−β
A block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
View SolutionA crate, in the form of a cube with edge lengths of 1.2 m, contains a piece of machinery, the center of mass of the crate and its contents is located 0.30 m above the crate's geometrical center. The crate rests on a ramp that makes an angle θ with the horizontal. As θ is increased from zero, an angle will be reached at which the crate will either tip over or start to slide down the ramp. If the coefficient of static friction between ramp and crate is 0.30, (a) does the crate tip or slide and (b) at what angle θ does this occur? If μs=0.70, (c) does the crate tip or slide and (d) at what angle θ does this occur? (Hint: At the onset of tipping, where is the normal force located?)
View SolutionA frictionless tracke ABCDE ends in a circular loop of radius 'r' A body slides down the track from the point 'A' which is at a height h=10 cm . The maximum value of 'r' for the body to successful complete the loop is

View SolutionA block of mass m height 2h and width 2b rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine

a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is μ.
b. the value of the acceleration at which block topples about A, assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of 20ms−1 with constant deceleration so that the block is not disturbed. The following data are given b=0.6m,h=0.9μ=0.5 and g=10ms−2
View SolutionTwo object are initially at rest on a frictionless surface. Object 1 has a greater mass than object 2. The same constant force start to act on each object. The force is removed from each object after it accelerates over a distance d. after the force is removed from both objects, which statement is correct (p:momentum, K: kinetic energy)?
View Solution
