If OABC is a tetrahedron such thatOA2+BC2=OB2+CA2=OC2+AB2 then
OA⊥BC
OB⊥AC
OC⊥AB
AB⊥AC
The correct Answer is:D
Step by step video, text & image solution for If OABC is a tetrahedron such thatOA^2 + BC^2 = OB^2 + CA^2 = OC^2 + AB^2 then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 1
13 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 2
19 Videos
- PROBABILITYBOOK - ARIHANT MATHSCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
55 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
OABC is a tetrahedron such that OA=OB=OC=k and each of the edges OA,OB and OCis inclined at an angle θ with the other two the range of θis
View SolutionIf G be the centroid of the ΔABCandO be any other point in theplane of the triangle ABC, then prove that: OA2+OB2+OC2=GA2+GB2+GB2+GC2+3GO2
View Solution
Knowledge Check
The OABC is a tetrahedron such that OA2+BC2=OB2+CA2=OC2+AB2,then
AOA⊥BCBOB⊥ACCOC⊥ABDAB⊥ACOABC is a parallelogram such that OA=a,OB=bandOC=c, then the value →OA.→BA is
Aa2+3b2+c22Ba2−b2+3c22Ca2+3b2−c22D3a2+b2−c22If a2+b2+c2−ab−bc−ca=0, then
Aa+b+c=0Ba=b=cCa=b=−cDa=−b=c
OABC is a tetrahedron D and E are the mid points of the edges −−→OA and −−→BC. Then the vector −−→DE in terms of −−→OA,−−→OBand−−→OC
View SolutionIn the figure shown, OABC is a rectangle with OA=3 units, OC = 4 units. If BD = 2.5 units, then the slope of the diagonal OB is equal to
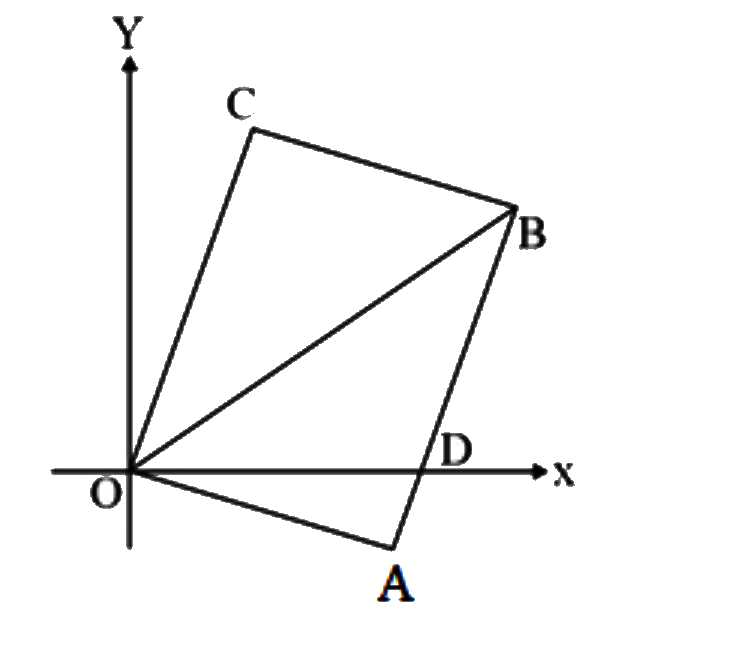
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
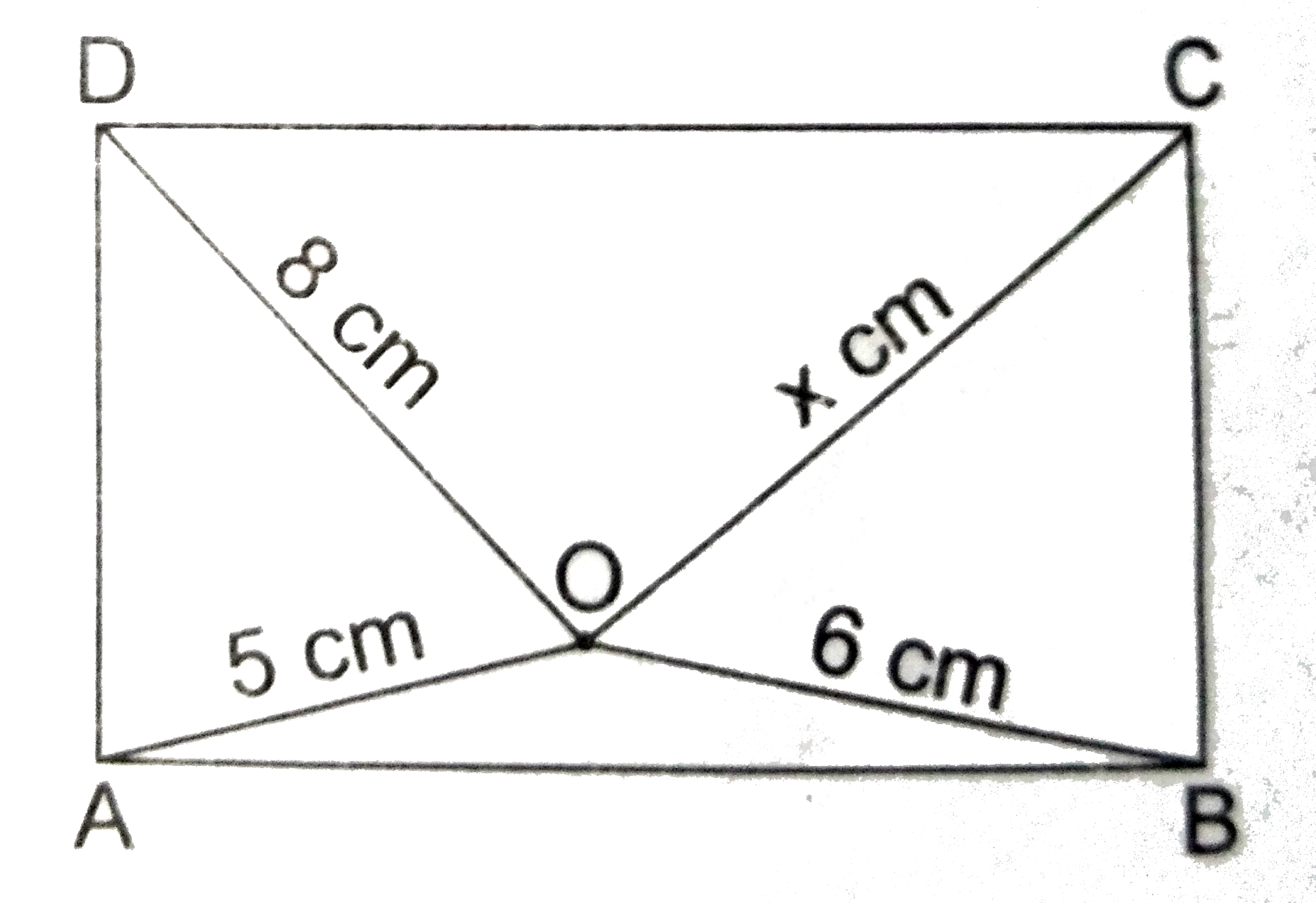
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
View SolutionIn the △OAB, M is the midpoint of AB, C is a point on OM, such that 2OC=CM. X is a point on the side OB such that OX = 2XB. The line XC is produced to meet OA in Y. Then OYYA=
View SolutionIf E is a point on side r:A of an equilateral triangle ABC such that BE⊥CA, then prove that AB2+BC2+CA2=4BE2.
View Solution
