Show that
is divisible by 1998
Video Solution
Text Solution
Here ,n = 1998 (Even )
Only result (i) applicable
Let
P is divisible by 37 .
Also
P is also divisaible by 54
Hence , P is divisible by , i.e, 1998.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - JEE Type Solved Example : (Matching Type Questions )2videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHSCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 18videos
BIONOMIAL THEOREM
- BOOK - ARIHANT MATHSCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)23videos
AREA OF BOUNDED REGIONS
- BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)16videos
CIRCLE
Similar Questions
Knowledge Check
- Question 1 - Select One
The value of 220001+219999220000−219998 is
A2B10/3C21000+1D10 - Question 2 - Select One
Question stimulus:-
Which one of the following four addresses is NOT EXACTLY the same as the one given below?
Robert S Ingram 1998 Revocable
8 Shaftsbury Ln
Hilton Head Island, SC 29926
(843) 342-7094
i. Robert S Ingram 1998 Revocable
8 Shaftsbury Ln
Hilton Head Island, SC 29926
(843) 342-7094
ii.Robert S Ingram 1998 Revocable
8 Shaftsbury Ln
Hilton Head Island, SC 29926
(843) 342-7094
iii. Robert S Ingram 1998 Revocable
8 Shaftsbury Ln
Hilton Head Island, SC 29926
(843) 342-7094
iv. Robert S Ingram 1998 Revocable
8 Shaftsbury Ln
Hilton Head Island, SC 29926
(843) 342-7094.AiBiiCiiiDiv - Question 3 - Select One
Following table gives the population of a from 1998 to 1992
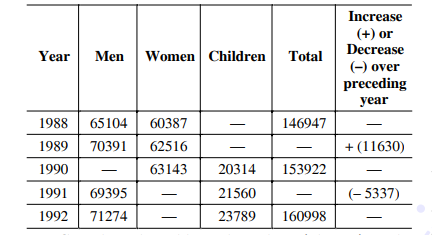
Number of children in 1989 is -----A25670B14040C13970D15702
The value of 22001+2199922000−21998,
View SolutionEvaluate.
(i) i1998
(ii)i−9999
(iii) (−√−1)4n=3,n ≠ NView SolutionNumber of workshops organized by a school in different areas during the last five years are as follows: years, No. of workshops 1995-1996 1996-1997 1997-1998 1998-1999 1999-2000, 25 30 42 50 65 Draw a histogram representing the above data.
View SolutionThe value of 1log2N+1log3N+1log4N+...+1log1988N is ; (N>0andN≠0) (i)1log1998(1N) (ii) logN(1998!) (iii) logN1998 (iv) none of these
View SolutionFollowing table gives the population of a from 1998 to 1992
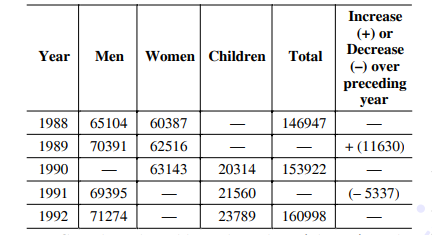
complete the table and mark a tick against the correct answer in each question
Number of men in 1990 is -----View Solution

