(d) यदि X={a,b,c},Y={1,2,3,4} एवं f={(a,4),(b,2),(c,3)},g={(a,1),(b,2),(c,3)(b,4)},h={(a,1),(b,2)}
तो f,g,h सम्मुच्य X से Y में फलन है या नहीं, बताएँ| फिर फलन का domain एवं range बताएँ|
The correct Answer is:केवल f है, domain = {a,b,c}, range ={2,3,4}
Step by step video, text & image solution for (d) यदि X={a,b,c}, Y={1,2,3,4} एवं f={(a,4),(b,2),(c,3)}, g={(a,1), (b,2), (c,3)(b,4)}, h={(a,1),(b,2)} तो f,g,h सम्मुच्य X से Y में फलन है या नहीं, बताएँ| फिर फलन का domain एवं range बताएँ| by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- फलन Book:DAS GUPTAChapter:फलन Exercise:सम्बन्ध और फलन पर विविध प्रश्न
Explore 8 Videos
- फलन Book:DAS GUPTAChapter:फलन Exercise:सम्बन्ध और फलन पर विविध प्रश्न
Explore 8 Videos
- प्रायिकता या संभाविता सिद्धांत की मूल संकल्पनाएँBook:DAS GUPTAChapter:प्रायिकता या संभाविता सिद्धांत की मूल संकल्पनाएँExercise:प्रश्नावली 1
Explore 46 Videos
- बिंदु, बिंदुपथ एवं इसका समीकरण Book:DAS GUPTAChapter:बिंदु, बिंदुपथ एवं इसका समीकरण Exercise:प्रश्नावली 1
Explore 10 Videos
Similar Questions
(a) R,N से N में एक सम्बन्ध है जहाँ R={(a,b):a∈N,b∈N और a=b2). निम्नलिखित में कौन-कौन सत्य है? सकारण बताएँ|
(i) (a,b)∈R, सभी a∈N के लिए ,
(ii) यदि (a,b) ∈R तो (b,a) ∈ R,
(iii) यदि (a,b)∈R,(b,c)∈R तो (a,c)∈R
(b) सम्बन्ध R={(x,x3):x<10,x} एक अभाज्य संख्या है| को सारणिबंध करें| फिर संबंध का प्राप्त और परास लिखें|
View Solution(a) R,N से N में एक सम्बन्ध है जहाँ R={(a,b):a∈N,b∈N और a=b2). निम्नलिखित में कौन-कौन सत्य है? सकारण बताएँ|
(i) (a,b)∈R, सभी a∈N के लिए ,
(ii) यदि (a,b) ∈R तो (b,a) ∈ R,
(iii) यदि (a,b)∈R,(b,c)∈R तो (a,c)∈R
(b) सम्बन्ध R={(x,x3):x<10,x} एक अभाज्य संख्या है| को सारणिबंध करें| फिर संबंध का प्राप्त और परास लिखें|
View Solutionदो सिक्कों की उछाल में (या एक सिक्के की दो उछालो मे) प्रायिकता समष्टि प्रदर्शित करे।
View Solutionउस बिंदु का बिंदुपथ निकले जिसकी दुरी बिंदु (1,2) से सदा 2 इकाई है।
View SolutionI A=[x,y,z],B=⎡⎢⎣ahghbfgfc⎤⎥⎦andC=[x,y,z]T,thenABC is (A) not defined (B) a 1×1 matrix (C) a 3×3 matrix (D) none of these
View SolutionConsider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.
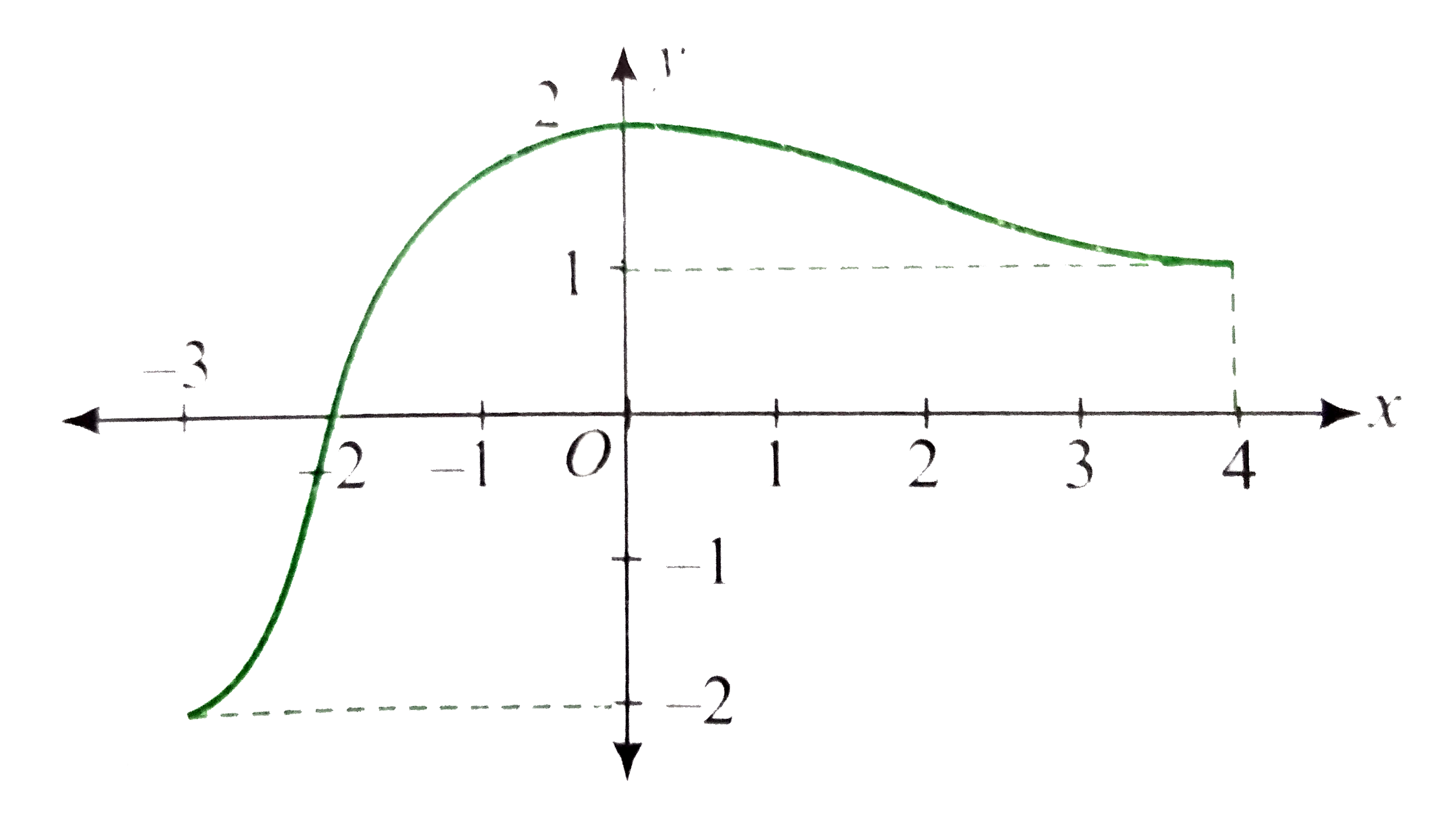
Domain and range of g(x)=f(|x|) is [a, b] and [c, d] respectively, then (b−a+c+d) is
View SolutionIf A=[xyz],B=⎡⎢⎣ahghbfgfc⎤⎥⎦ and C=⎡⎢⎣xyz⎤⎥⎦
Then ABC=O if
View SolutionLet X = { 1,2,3,4}, Y = {a,b,c,d} and f={(1,a), (4,b), (2,c),(3,d),(2,d)}. Then f is
View SolutionयदिA=[xyz],B=⎡⎢⎣ahghbfgfc⎤⎥⎦ तथा C=⎡⎢⎣xyz⎤⎥⎦ तो का ABC मान ज्ञात कीजिए।
View SolutionX={(1,2,3,4},Y={a,b,c,d}மற்றும் f={(1,a),(4,b),(2,c),(3,d),(2,d)}எனில் f என்பது
View SolutionIf f(x)={(|x|−3 when x<1), and (|x−2|+a, when x≥1) &
g(x)={2−|x|when x<2 and sgn(x)−b , when x≥2.
if h(x)=f(x)+g(x) is discontinuous at exactly one point, then -
(a). a=−3,b=0
(b). a=−3,b=−1
(c) a=2,b=1
(d) a=0,b=1
View SolutionConsider a function f whose domain is [-3, 4] and range is [-2, 2] with following graph.

Domain and range of g(x)=f(|x|) is [a, b] and [c, d] respectively, then (b−a+c+d) is
View SolutionAssertion (A) : If f(x) , g(x) and h(x) are continueous on [a,b] and differentiable in (a,b) , then, the exists c∈(a,b) such that ∣∣ ∣ ∣∣f(a)g(a)h(a)f(b)g(b)h(b)f'(c)g'(c)h'(c)∣∣ ∣ ∣∣=0
Reason ( R ) : Lagrange's Mean Value theorem is applicable on [a,b] for ϕ(x)=∣∣ ∣ ∣∣f(a)g(a)h(a)f(b)g(b)h(b)f'(c)g(x)h(x)∣∣ ∣ ∣∣=0
Then , which of the following is true?
View SolutionWhat should come next in the following letter series ?
H G F E D C B A H G F E D C B A H G F E D C B A H ?
1) G
2) E
3) A
4) I
5) None of these
View SolutionLet f={(1,a),(2,b),(3,c),(4,d)} and g={(a,x),(b,x),(c,y),(d,x)} Determine gof and fog if possible. Test whether fog=gof.
View Solution

