एक चतुर्भुज ABCD के विकर्ण परस्पर लम्ब है। सिद्ध कीजिए कि इसकी भुजाओं के मध्य बिंदुओं को मिलाने वाले रेखाखण्डों से एक आयत बनता है।
माना □ABCD की भुजाओं AB,BC,CD और DA के मध्य बिंदु क्रमशः P,Q,R और S है।
ΔABC में
AB का मध्य बिंदु P है।
BC का मध्य बिंदु Q है।
∴PQ∣∣AC और PQ=12AC…………1
इसी प्रकार
RS∣∣AC और RS=12AC ...........2
समीकरण 1 और 2 से
PQ∣∣RS और PQ=RS
⇒□PQRS एक समांतर चतुर्भुज है।
माना □ABCD के विकर्ण AC और BD एक-दूसरे को O पर काटते हैं।
ΔABD में
P,AB का मध्य बिंदु और S,AD का मध्य बिंदु है
∴PS∣∣BD
⇒PN∣∣MO
इसी प्रकार PQ∣∣AC
⇒PM∣∣NO
∴□PMON एक समांतर चतुर्भुज है।
⇒∠MPN=∠MON
⇒∠MPN=∠BOA
⇒∠MPN=90∘(∵∠BOA=90∘,AC⊥BD)
⇒∠QPS=90∘
अब □PQRS एक समांतर चतुर्भुज है। जिसका एक कोण 90∘ है।
∴□PQRS एक आयत है।

Topper's Solved these Questions
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8A
27 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8B
15 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
Similar Questions
एक चतुर्भुज के दो कोणों 89∘ और 113∘ है। यदि अन्य दो कोण बराबर है तो बराबर कोणों को ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।
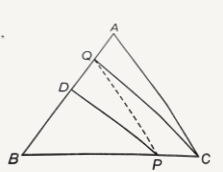
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
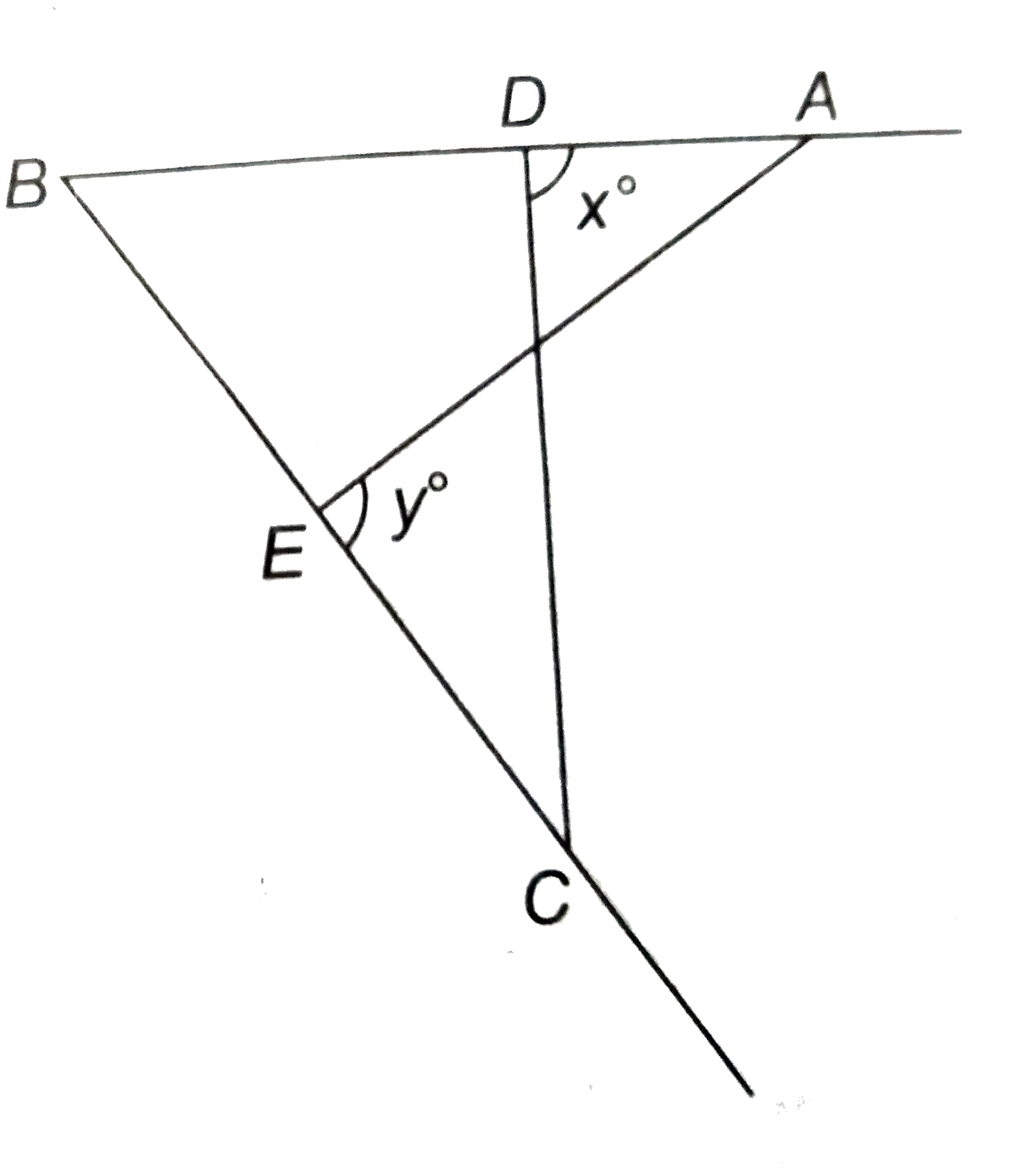
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionसिद्ध कीजिए कि बिंदुओं (2,3) और(3,4) को मिलाने वाले रेखाखण्ड के मध्य बिंदु के निर्देशांक x और y निम्नलिखित समीकरण को संतुष्ट करते है :
x−y+1=0.
View SolutionL लम्बाई की एक छड़ जिसके सिरे दो परस्पर लम्ब रेखाओं पर स्थित है , फिसलती है । छड़ को 1:2 के अनुपात में विभाजित करने वाले बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionपरवलय y2=4px की किसी द्विकोटि की लम्बाई 8p है। सिद्ध कीजिए कि शीर्ष को उसके सिरों से मिलाने वाली सरल रेखाएँ परस्पर लम्ब है।
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solution
