संलग्न चित्र में, ABCD एक समान्तर चतुर्भुज है, ABM एक रेखा खण्ड है और E, BC का माध्य-बिन्दु है। सिद्ध कीजिए कि :
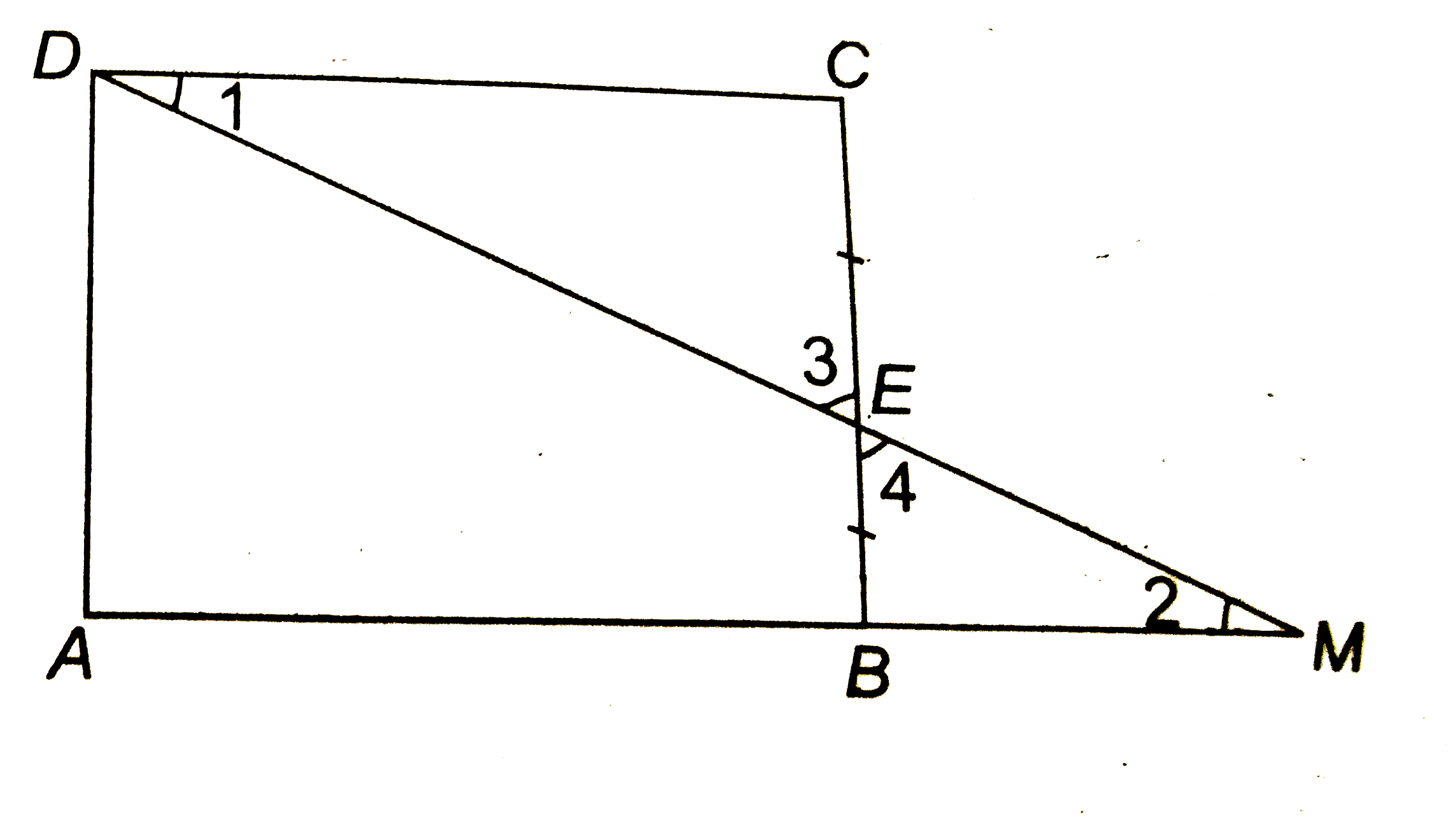
(i) ΔDCE≅ΔMBE
(ii) AB=BM
(iii) AM=2DC
(i) ∵ABCD एक समान्तर चतुर्भुज है।
∴ABM∣∣DC
∴∠1=∠2 (एकान्तर कोण)
अब ΔDCE और ΔMBE में,
⎧⎪
⎪⎨⎪
⎪⎩∠1=∠2 (ऊपर सिद्ध किया है)∠1=∠4 (शीर्षाभिमुख कोण )CE=BE (दिया है कि E माध्य-बिन्दु है)
∴ΔDCE≅ΔMBE (A.A.S.)
(ii) अतः DC=MB (c.p.c.t.)
परन्तु DC=AB (समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती है)
∴AB=MB
(iii) अब, AM=AB+BM
=DC+DC (ऊपर सिद्ध किया है)
=2DC
Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - साधित उदाहरण
11 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7A
30 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - विविध प्रश्नावली
12 Videos
Similar Questions
ΔABC में, ∠A=100∘,∠C=30∘ है। ΔABC (i) सबसे बड़ी (ii) सबसे छोटी भुजा कौन-सी है?
View Solutionनिम्नलिखित में से कौन-से त्रिभुजों के युग्म सर्वांगसम है ? प्रत्येक में सर्वागसमता का प्रतिबन्ध भी बताइए :
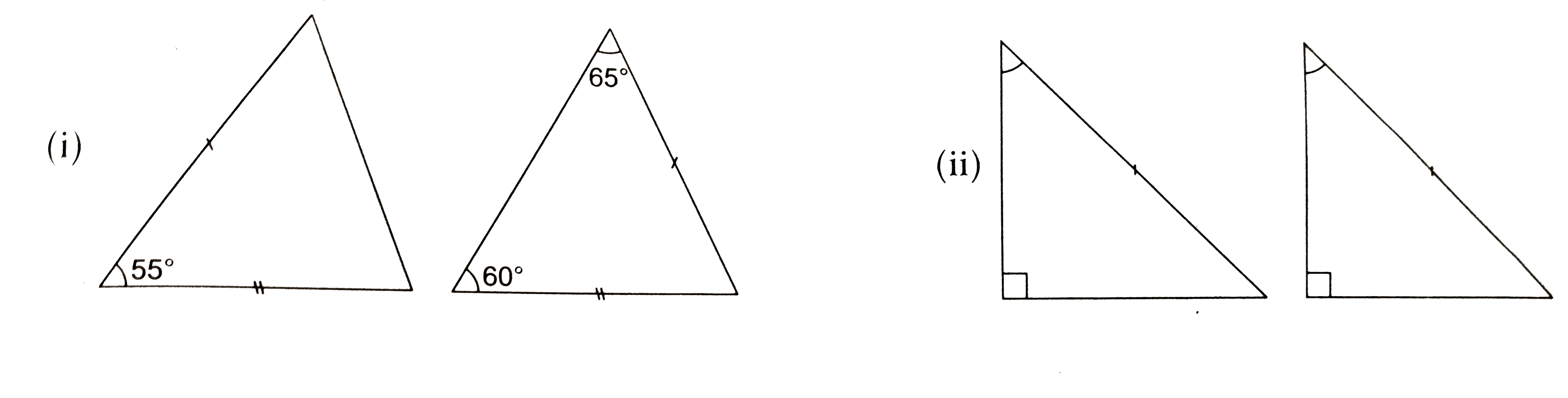
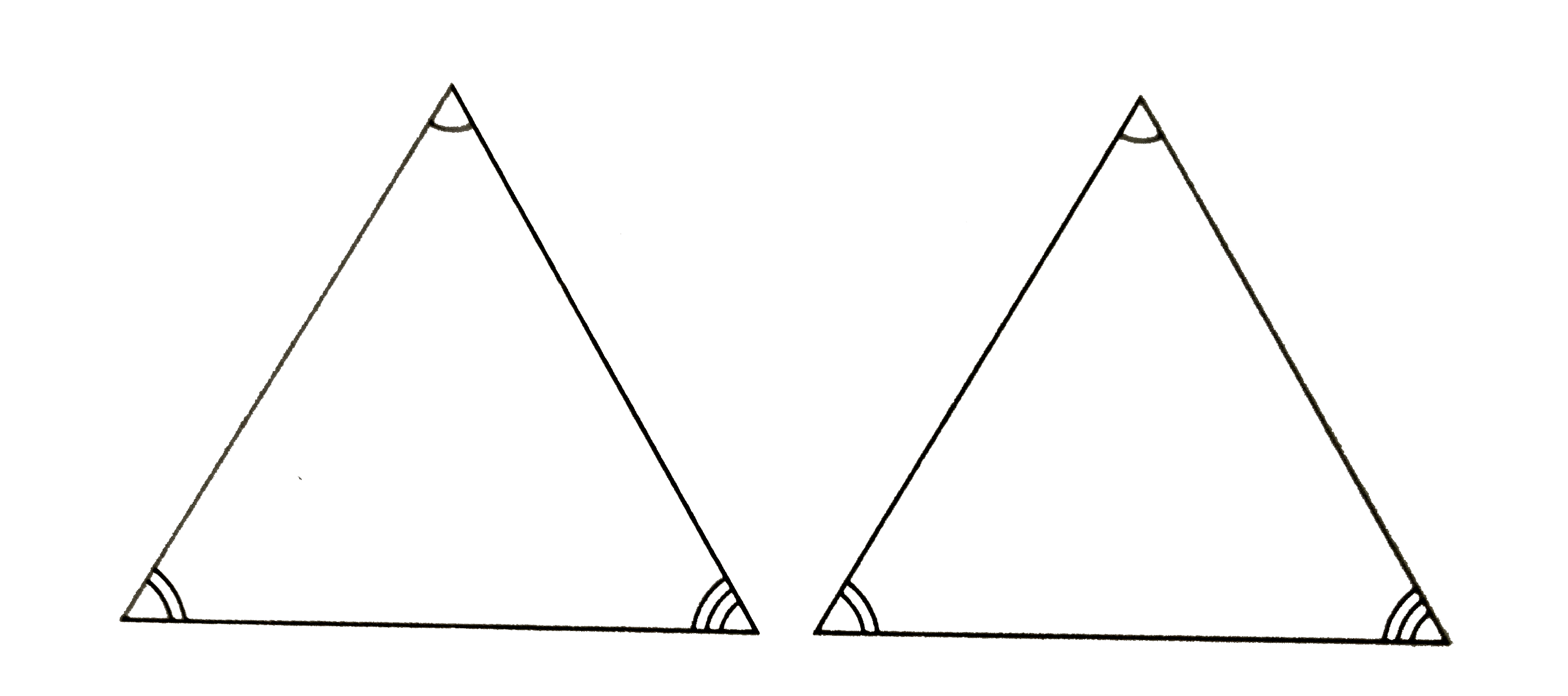
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
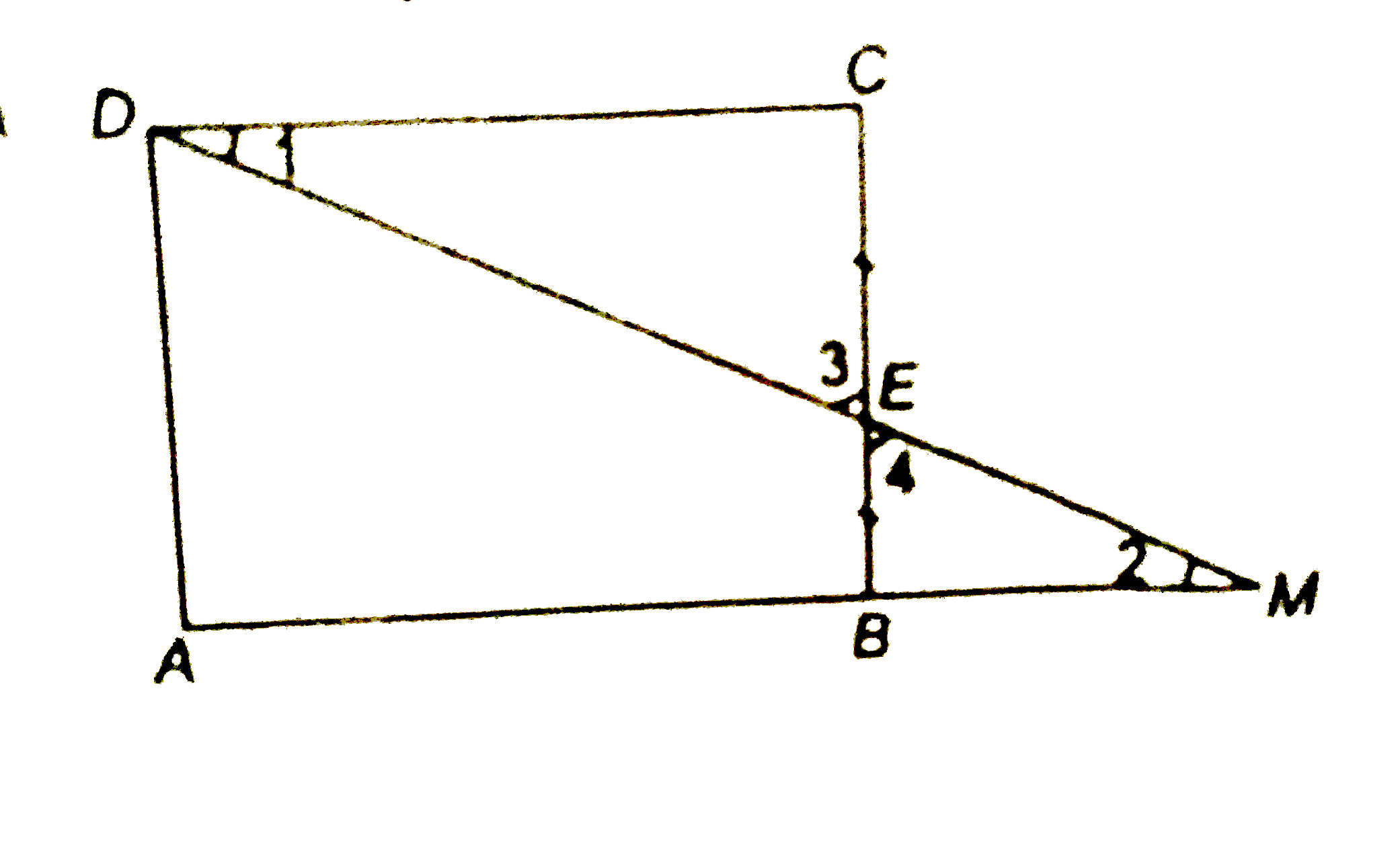
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View Solution
