A beam of natural light falls on the surface of glass at an angle of $45^{\circ}$ . Using the Fresnel equations, find the degree of polarization of
(a) reflected light,
(b) refracted light.

Video Solution

Text Solution

Verified by Experts

Here $θ_{1} = 45^{\circ}$
${sin θ}_{2} = \frac{1}{\sqrt{2}} \times \frac{1}{n} = \frac{2}{3 \sqrt{2}} = \frac{\sqrt{2}}{3} = 0.4714$
$θ_{2} = {sin}^{- 1} 0.4714 = {28.1}^{\circ}$
Hence $I'_{⊥} = I_{⊥} \frac{{sin}^{2} (θ_{1} - θ_{2})}{{sin}^{2} (θ_{1} + θ_{2})}$
$= \frac{1}{2} I_{0} {(\frac{{sin 16.9}^{\circ}}{{sin 73.1}^{\circ}})}^{2} = \frac{1}{2} I_{0} \times 0.0923$
Thus $I'_{∣ ∣} = \frac{1}{2} I_{0} {(\frac{{tan 16.9}^{\circ}}{{tan 73.1}^{\circ}})}^{2} = \frac{1}{2} I_{0} \times 0.0085$
(a) Degree of polarization $P$ of the reflected light
$= \frac{0.0838}{0.1008} = 0.831$
(b) By conservation of energy
$I''_{⊥} = \frac{1}{2} I_{0} \times 0.9077$
$I''_{∣ ∣} = \frac{1}{2} I_{0} \times 0.9915$
Thus $P = \frac{0.0838}{1.8982} = 0.044$

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A beam of light is incident on glass slab making an angle of $60^{\circ}$ with the surface. The angle of refraction and the velocity of light in glass of R.I. 1.5 are
A $19^{\circ} 28, 3 \times 10^{8} m / s$
B $29^{\circ} 28', 2 \times 10^{8} m / s$
C $19^{\circ} 28', 2 \times 10^{8} m / s$
D $29^{\circ} 28, 3 \times 10^{8} m / s$
Question 2 - Select One
Figure represents a glass plate placed vertically on a horizontal table with a beam of unpolarised light falling on its surface at the polarising angle of $57^{\circ}$ with the normal. The electric vector in the reflected light on screen S will vibrate with respect to the plane of incidence in a

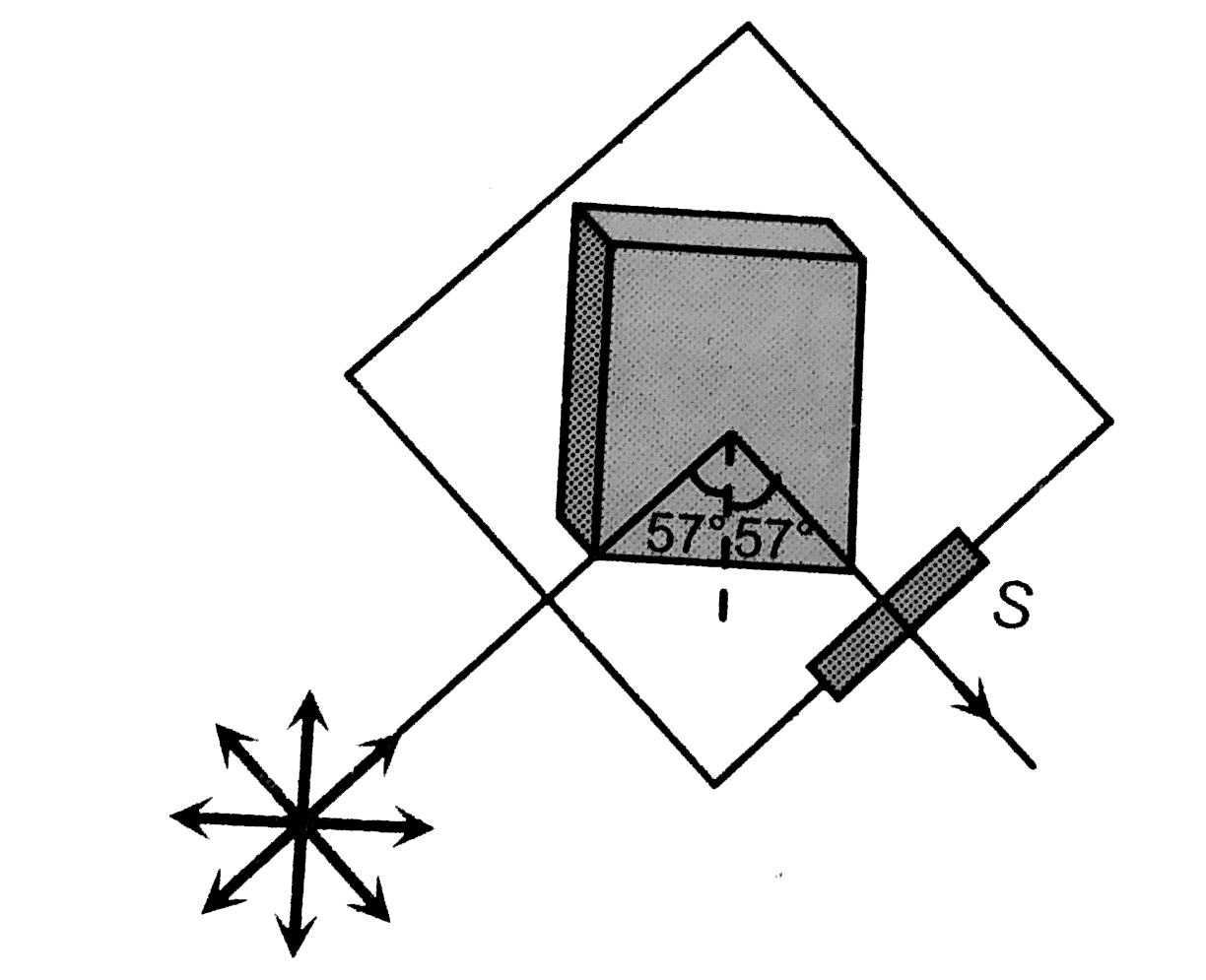A(a) Vertical plane
B(b) Horizontal plane
C(c) Plane making an angle of $45^{\circ}$ with the vertical
D(d) Plane making an angle of $57^{\circ}$ with the horizontal
Question 3 - Select One
A ray of light is incident on a glass slab at an angle of $45^{\circ}$ . If refractive index of glass be 1.6, what is the angle of refraction ?
A ${45.2}^{\circ}$
B $30^{\circ}$
C ${26.2}^{\circ}$
D ${15.2}^{\circ}$

IE IRODOV, LA SENA & SS KROTOV-OPTICS-Polarization Of Light

Home
Ask Doubt
Profile