By means of plotting find the amplitude of the oscillation resulting from the addition of the following three oscillations of the same direction:
ξ1=acosωt,ξ2=2asinωt,ξ3=1.5acos(ωt+π/3).
It is easier to do it analytically.
ξ1=acosωt,ξ2=2asinωt
ξ3=32a(cos.π3cosωt−sin.π3sinωt)
Resultant vibration is
ξ=7a4cosωt+a(2−3√34)sinωt
This has an amplitude =a4√49×(8−3√3)2=1.89a
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
Using graphical means find an amplitude a of oscillations resulting from the superposition of the following oscillations of the same direction :
(a)x1=3.0cos(ωt+π/3),x2=8.0sin(ωt+π/6),
(b) x1=3.0cosωt,x2=5.0cos(ωt+π/4),x3=6.0sinωt.
View SolutionIf current 11=3A sin ωtand12=4Acosωt,then13 is
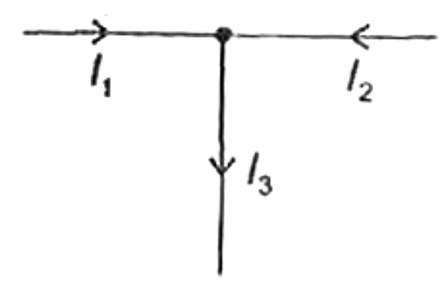
View Solution
Knowledge Check
Find the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωtA5B10C15D20The resultant amplitude due to super position of x1=sinωt,x2=5sin(ωt+37∘) and x3=−15cosωt is :
A17B21C13DNone of theseWhich two of the given transverse waves will give stationary wave when get superimposed?
z1=acos(kx−ωt) (A)
z2=acos(kx+ωt) (B)
z3=acos(ky−ωt) (C)AA and BBA and CCB and CDAny two
What kind of polarizations has a plane electromagetic wave if the projections of the vector E on the x and y axes are perpendicular to the propagation direction and are defind by the following equations:
(a) Ex=Ecos(ωt−kz),Ey=Esin(ωt−kz),
(b) Ex=Ecos(ωt−kz),Ey=Ecos(ωt−kz+π/4)
(c) Ex=Ecos(ωt−kz),Ey=Ecos(ωt−kz+π)?
View SolutionFind the displacement equation of the simple harmonic motion obtained by combining the motions.
x1=2sinωt,x2=4sin (ωt+π6)
and x3=6sin(ωt+π3)
View SolutionIn the given figure, if i1=3sinωtandi2=4cost, then i3 is
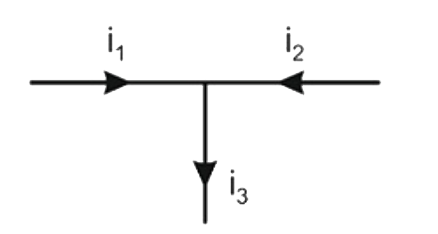
View SolutionA certain oscillation results from the addition of coherent oscillations of the same direction y=acos[ωt+(k−1)ϕ] where k is the number of oscillation [ k=1,2………N] and ϕ is the phase difference between kthand(K−1)th oscillations. The amplitude of resultant oscillation will be
View SolutionTwo waves y1=asin(ωt−kx) and y2=acos(ωt−kx) superimpose at a point :
View Solution
