A certain luminous surface obeys Lambert's law. Its luminance is equal to L. Find:
(a) the luminous flux emitted by a element ΔS of this surface into a cone whose axis is normal to the given element and whose aperture angle is equal to θ,
(b) the luminosity of such a source.
For a Lambert source L= const The flux emitted into the cone is
Φ=LΔScosαdΩ
=LΔS∫θ02πcosαsinαdα
=LΔSπ(1−cos2θ)=πLδSsin2θ
(b) The luminosity is obtained from the pervious fromula for θ=90∘
M=Φ(θ=90∘)ΔS=πL

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
A Lamber source has a luminance L. Find:
(a) the luminuous flux emitted by an element ΔS of this surface into the forward cone along the normal toΔS and of semivertical angleθ,
(b) the luminosiy of such a source.
View SolutionA Lambert source has the from of an infinite plane. Its luminance is equal to L. Find the illuminance of an area element oriented parallel to the given source.
View SolutionDetermine the luminosity of a surface whose luminance depends on direction as L=L0cosθ, where θ is the angle between the radiation direction and the normal to the surface.
View SolutionThe magentic induction in vacumm at a plaen surface of a magentic is equal to B and the vector B forms an angle θ with the normal n of the surface (Fig). The permeability of the magnetic is equal to μ. Find:
(a) the flux of the vector H through the spherical surface S of radius R, whose centre lies on the surface of the magentic,
(b) the circulation of the vector B around the square path I' widh side l located as shwon in the fig.

View SolutionThe magnetic induction in vacumm at a plane surface of a uniform istropic magnetic is equal to B, the vector B forming an angle α with the normal of the surface. The permeability of th emagnetic is equal to μ. Find the magnitic of the magnetic induction B in the magnetic in the vicinity of its surface.
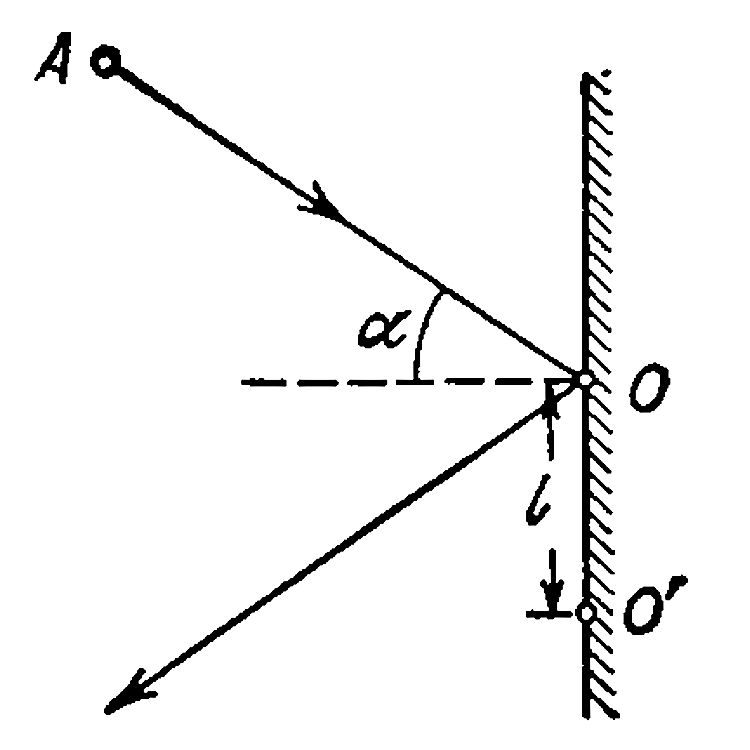
View SolutionA disc A of mass m sliding over a smooth horizontal surface with velocity v experiences a perfectly elastic collision with a smooth stationary wall at a point O (figure). The angle between the motion direction of the disc and the normal of the wall is equal to α. Find:
(a) the points relative to which the angular momentum M of the disc remains constant in this process,
(b) the magnitude of the increment of the vector of the disc's angular momentum relative to the point O′ which is located in the plane of the disc's motion at the distance l from the point O.
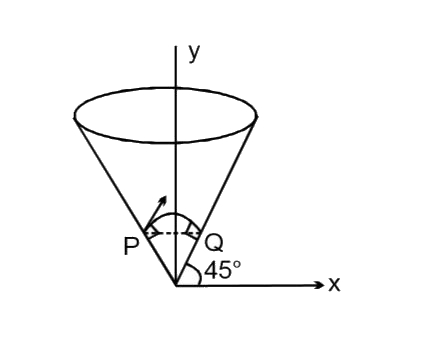
View SolutionA particle is projected from point P with velocity 5√2m/s perpendicular to the surface of a hollow right angle cone whose axis is vertical. It collides at Q normally. Find the time of the flight of the particle.
View SolutionA point source emitting uniformly in all directions is placed above a table top at a distance of 0.50 m from it. The luminous flux of the source is 1570 lumen. Find the illuminance at a small surface area of the table to a.directly below the source and b. at as distance of 0.80 m from the source.
View SolutionA point source emitting light uniformly in all directions is placed above a table-top at a distance of 0.50m from it. The luminous flux of the source is 1570 lumen. Find the illuminace at a small surface area of the table top (i) directly above the source and (ii) at a distance of 0.80 m from the source.
View SolutionNear the point plane surface of a uniform isotropic dielectric with permittivity ε the electric field strength in vacumm is equal to E0 the vector E0 forming an angle θ with the normal of the dielectric's surface (FIg). Assuming the field to be uniform both inside and outside the dielectric, Find:

(a) the flux of the vector E through a sphere of radius R with centre located at the surface of the dielectric,
(b) the circulation of the vector D around the closed path I' og length l (see fig) whose plane is perpendicular to the surface of the dielectric and parallel to the vector E0.

View Solution
