A rotating disc moves in the positive direction of $x$ -axis as shown. Find the equation $y (x)$ describing the position of the instantaneous axis of rotation if at the initial moment the centre $C$ of the disc was located at origin after which (a) it moved with constant acceleration a (initial velocity zero) while the disc rotating anticlockwise with constant angular velocity $ω$ . (b) it moved with constant velocity $v$ while the disc started rotating anticlockwise with a constant angular acceleration a (with initial angular velocity zero).

Video Solution

Text Solution

Verified by Experts

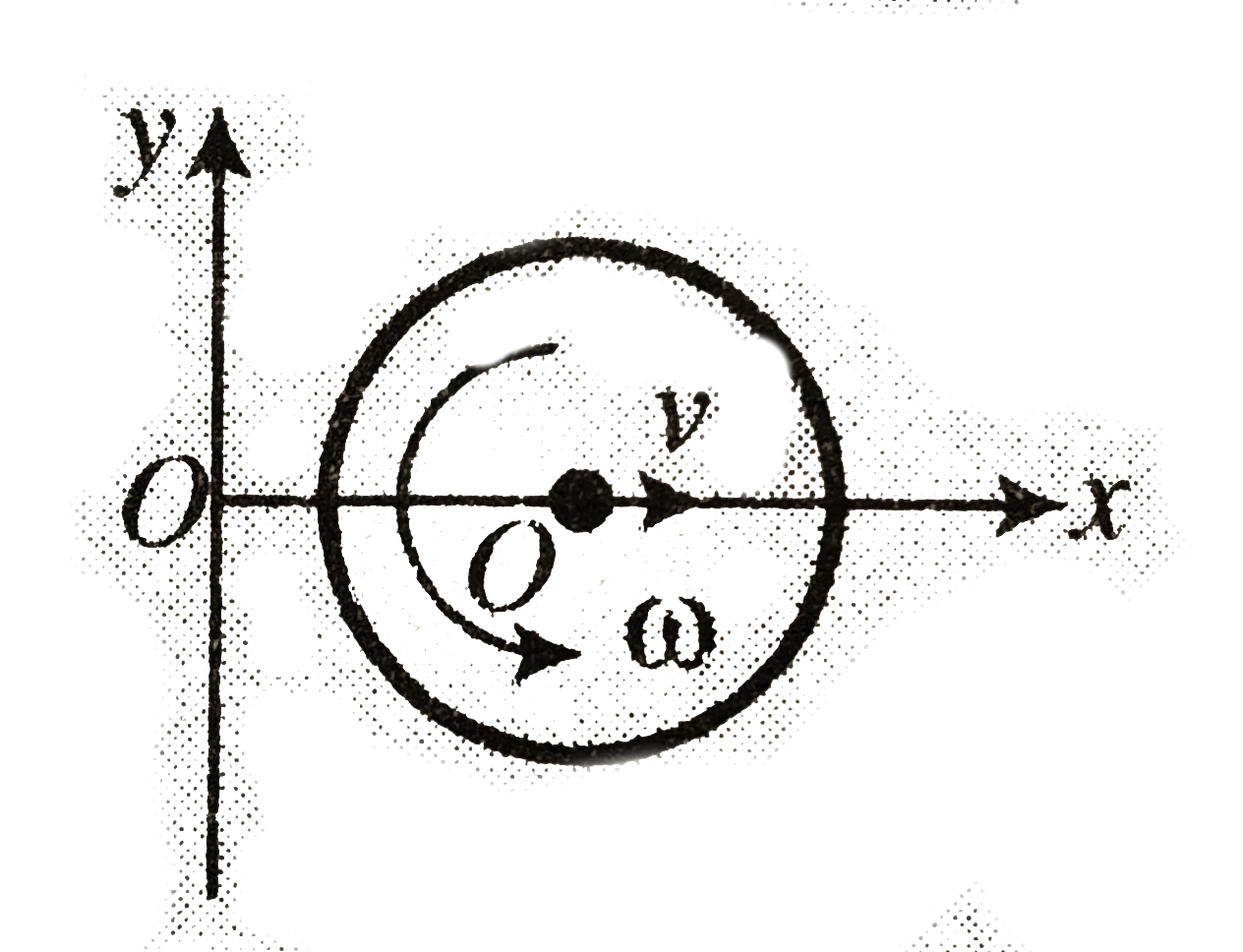
Rotating disc moves along the x-axis, in plane motion in $x - y$ plane. Plane motion of a solid can be imagined to be in pure rotation about a point (say I) at a certain instant known as instantaneous centre of rotation. The instantaneous axis whose positive sense is directed along $\to ω$ of the solid and which passes through the point I, is known as instantaneous axis of rotation.
Therefore the velocity vector of an arbitrary point $(P)$ of the solid can be represented as:
${\to v}_{P} = \to ω \times {\to r}_{P I}$ (1)
On the basis of Eq. (1) for the C.M. (C) of the disc
${\to v}_{c} = \to ω \times {\to r}_{d}$ (2)
According to the problem ${\to v}_{c} ↑ ⏐ ⏐ ↑ ⏐ ⏐ \to i$ and $\to ω ↑ ⏐ ⏐ ↑ ⏐ ⏐ \to k$ i.e., $\to ω ⊥ x - y$ plane, so to satisfy the Eqn. (2) ${\to r}_{C I}$ is directed along $(- \to j)$ . Hence point I is at a distance $r_{C I} = y$ , above the centre of the disc along y-axis. Using all these facts in Eq. (2), we get
$v_{C} = ω y$ or $y = \frac{v_{c}}{ω}$ (3)
(a) From the angular kinematical equation
$ω_{z} = ω_{0 z} + β_{z} t$ (4)
$ω = β t$ .
On the other hand $x = v t$ , (where x is the x coordinate of the C.M.)
or, $t = \frac{x}{v}$ (5)
From Eqs. (4) and (5), $ω = \frac{β x}{v}$
Using this value of $ω$ in Eq. (3) we get $y = \frac{v_{c}}{ω} = \frac{v}{β x / v} = \frac{v^{2}}{β x}$ (hyperbola)
(b) As centre C moves with constant acceleration $w$ , with zero initial velocity
So, $x = \frac{1}{2} w t^{2}$ and $v_{c} = w t$
Therefore, $v_{c} = w \sqrt{\frac{2 x}{w}} = \sqrt{2 x w}$
Hence $y = \frac{v_{c}}{ω} = \frac{\sqrt{2 w x}}{ω}$ (parabola)

Updated on:21/07/2023

|

Class 12 PHYSICS PHYSICAL FUNDAMENTALS OF MECHANICS

Topper's Solved these Questions

Similar Questions

IE IRODOV, LA SENA & SS KROTOV-PHYSICAL FUNDAMENTALS OF MECHANICS-Relativistic Mechanics

Home
Ask Doubt
Profile