A 20 V battery of internal resistance $1 Ω$ is connected to three coils of $12 Ω, 6 Ω$ , and $4 Ω$ in parallel, a resistor of $5 Ω$ and a reversed battery (emf $8 V$ and internal resistance $2 Ω$ ) as shown in figure. Calculate $(a)$ the current in the circuit, $(b)$ current in resistor of $12 Ω$ coil, and $(c)$ potential difference across each battery.

Video Solution

Text Solution

Verified by Experts

Equivalent resistance R' of $12 Ω, 6 Ω$ and $4 Ω$ connected in parallel is
$\frac{1}{R}' = \frac{1}{12} + \frac{1}{6} + \frac{1}{4} = \frac{6}{12} = \frac{1}{2} or R' = 2 Ω$
Total resistance of circuit, $R = 1 + 5 + 2 + 2$
$= 10 Ω$
Effective emf of circuit $= 20 - 8 = 12 V$
Current in the circuit $I = \frac{12}{10} = 1.2 A$
So, current through each battery and $5 Ω$ resistor, $= 1.2 A$
Pot. diff. across the parallel combination of three resistors, $V' = I R' = 1.2 \times 2 = 2.4 V$
Current in $12 Ω$ coil = $\frac{2.4}{12} = 0.2 A$
Current in $6 Ω$ coil = $\frac{2.4}{6} = 0.4 A$
Current in $4 Ω$ coil = $\frac{2.4}{4} = 0.6 A$
Terminal pot. diff. across 20 V battery
$V = ε - I r = 20 - 1.2 \times 1 = 18.8 V$
Terminal pot. diff. across8 V battery
$V' = ε' + I r' = 8 + 1.2 \times 2 = 10.4 V$

Updated on:21/07/2023

A battery of e mf 10 V and internal resistance $3 Ω$ is connected to a resistor as shown in the figure. If the current in the circuit is 0.5 A . then the resistance of the resistor will be

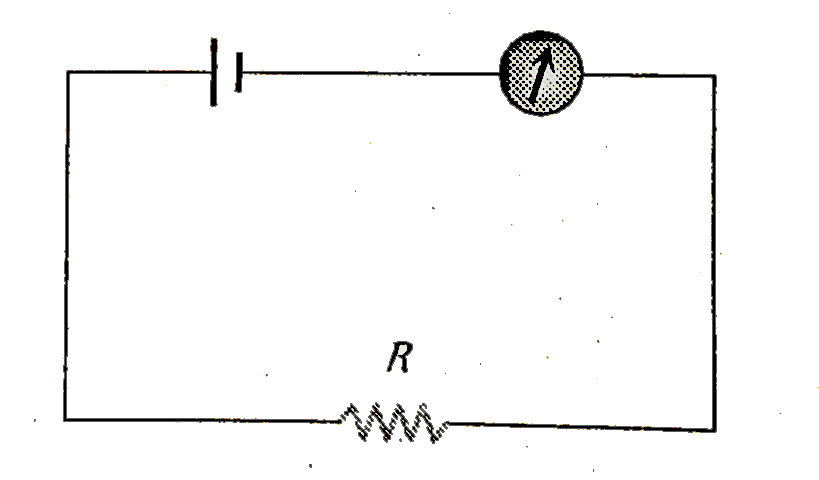A $19 Ω$
B $17 Ω$
C $10 Ω$
D $12 Ω$
A battery of emf 15 V and internal resistance of $4 Ω$ is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A $2.5 Ω, 6 V$
B $3.5 Ω, 6 V$
C $2.5 Ω, 7 V$
D $3.5 Ω, 7 V$
Two heating coils of resistance $10 Ω and 20 Ω$ are connected in parallel and connected to a battery of emf 12V and internal resistance $1 Ω$ . The power consumed by them is in the ratio
A $1 : 4$
B $1 : 3$
C $2 : 1$
D $4 : 1$