Eight identical point charges of q coulomb each are placed at the corners of a cube side 0.1m. Calculate electric field at the centre of the cube. Calculate the field at the center when one of the corner charges is removed.
The correct Answer is:Zero ; (1.2×1012q)NC−1 towards the corner without charge
To solve the problem of finding the electric field at the center of a cube with point charges at its corners, we will follow these steps:
Step 1: Understand the Configuration
We have a cube with side length a=0.1m and 8 identical point charges q placed at each corner of the cube.
Step 2: Calculate the Electric Field at the Center with All Charges
The electric field →E due to a point charge q at a distance r is given by the formula:
→E=kqr2^r
where k=9×109N m2/C2 is Coulomb's constant.
The distance from each corner of the cube to the center of the cube can be calculated using the formula for the body diagonal of a cube:
r=a√32
For our cube, this becomes:
r=0.1√32≈0.0866m
Step 3: Determine the Electric Field Contribution from Each Charge
Each charge contributes to the electric field at the center. However, due to symmetry, the contributions from opposite charges will cancel each other out.
Since there are 8 charges symmetrically placed, the net electric field at the center of the cube is:
→Enet=0
Step 4: Calculate the Electric Field at the Center When One Charge is Removed
Now, if we remove one charge from one corner, we are left with 7 charges. The remaining charges will still be symmetrically placed around the center, but now there will be an imbalance.
Step 5: Determine the Direction of the Electric Field
The electric field at the center due to the remaining 7 charges will point towards the empty corner (where the charge was removed).
Step 6: Calculate the Electric Field Due to One Charge
The electric field at the center due to one charge q at the corner is given by:
→E=kqr2
Substituting r=0.0866m:
→E=kq(0.0866)2
Step 7: Calculate the Total Electric Field Due to 7 Charges
The total electric field at the center due to the 7 charges can be calculated as:
→Etotal=7⋅→E=7⋅kq(0.0866)2
This electric field will point towards the empty corner.
Final Result
The electric field at the center of the cube with all charges is 0N/C. When one charge is removed, the electric field at the center is directed towards the corner where the charge was removed and has a magnitude of:
→Etotal=7⋅kq(0.0866)2
We have a cube with side length a=0.1m and 8 identical point charges q placed at each corner of the cube.
The electric field →E due to a point charge q at a distance r is given by the formula:
→E=kqr2^r
where k=9×109N m2/C2 is Coulomb's constant.
r=a√32
For our cube, this becomes:
r=0.1√32≈0.0866m
Each charge contributes to the electric field at the center. However, due to symmetry, the contributions from opposite charges will cancel each other out.
→Enet=0
Now, if we remove one charge from one corner, we are left with 7 charges. The remaining charges will still be symmetrically placed around the center, but now there will be an imbalance.
The electric field at the center due to the remaining 7 charges will point towards the empty corner (where the charge was removed).
The electric field at the center due to one charge q at the corner is given by:
→E=kqr2
Substituting r=0.0866m:
→E=kq(0.0866)2
The total electric field at the center due to the 7 charges can be calculated as:
→Etotal=7⋅→E=7⋅kq(0.0866)2
This electric field will point towards the empty corner.
The electric field at the center of the cube with all charges is 0N/C. When one charge is removed, the electric field at the center is directed towards the corner where the charge was removed and has a magnitude of:
→Etotal=7⋅kq(0.0866)2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Four point charges of +1μc each are placed on the four corners of a square of side 1 m. Calculate the electric potential at the centre of the square.
View SolutionSix equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
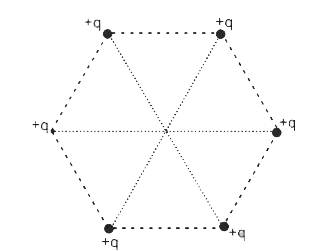
View Solution
Knowledge Check
A charge 'Q' is placed at each corner of a cube of side 'a'. The potential at the centre of the cube is
A8Qπε0aB4Q4πε0aC4Q√3πε0aD2Qπε0aA charge of q μC is placed at the centre of a cube of side 0.1 m. the electric flux diverging from each face of the cube will be
Aq×10−6ε0 VmBq×10−66ε0 VmC6q×10−6ε0VmDq×10−4(ε0)VmIf 8 identical charges of -g each are placed at the eight corners of a cube of side b, then electrostatic potential energy of a charge +q0 placed at the centre of the cube will be
A8√2qq04πε0bB−8√2qq04πε0bC+4qq0√3πε0bD−4qq0√3πε0b
Four point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.

View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionA charge Q is placed at the centre of a cub. Find the flux of the electric field through the six surfaced of the cube.
View SolutionA point charge of 10−7C is situated at the centre of a cube of side 1m. Calculate the electric flux through its surface.
View Solution
