The following figure from shows version of a zoom.The converging lens has a focal length $f_{1}$ and the diverging lens has focal length $f_{2} = - | f_{2} |$ .the two lens are separated by a variable distance d that it is always less than $f_{1},$ also the magnitude of the focal length of the diverging lens satisfies the inequality
$| f_{2} | > (f_{1} - d) .$

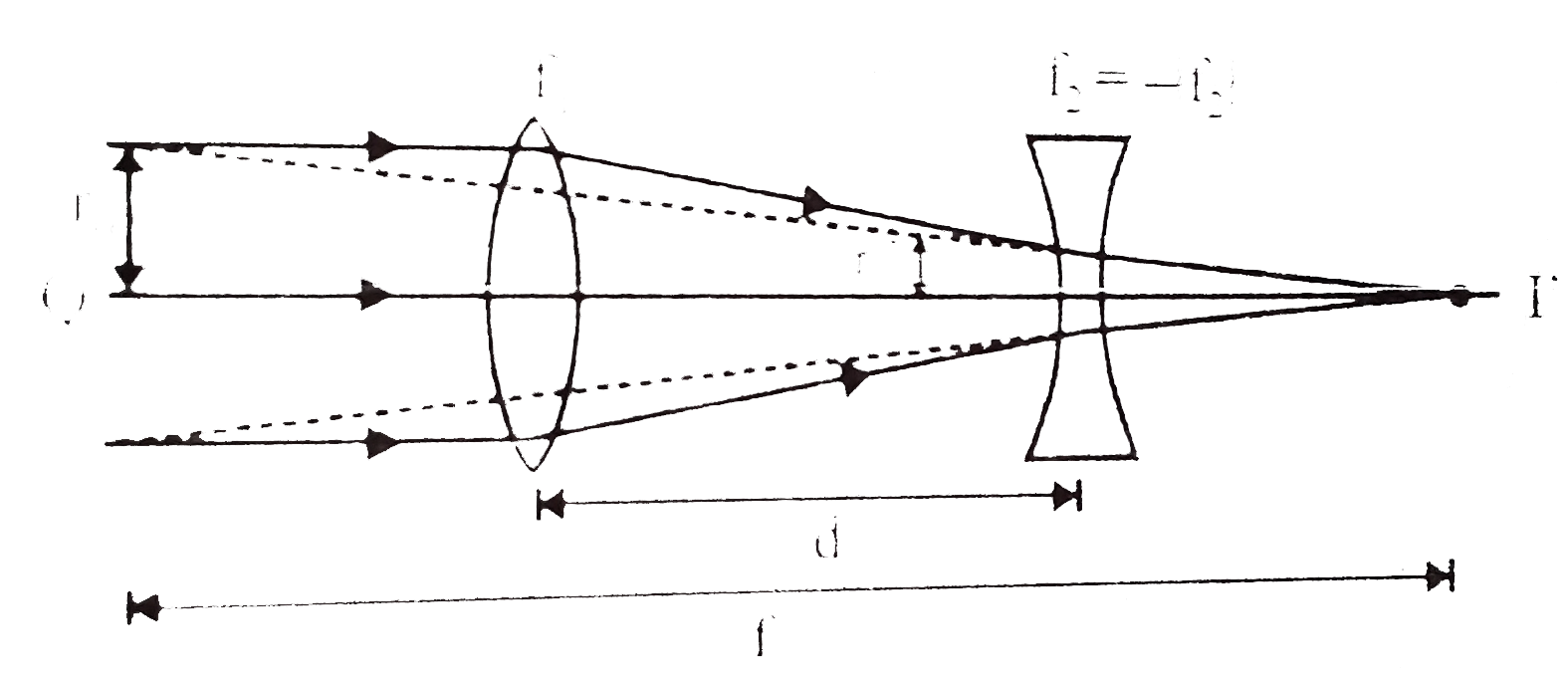
if the rays that emerge form the diverging lens and reach the final image point are extended backward to the left of the diverging lens,they will eventually expand to the original radius $r_{o}$ at the same point. $Q$ .To determine the effective focal length of the combination lens consider a bundle of parallel rays of radius $r_{0}$ entering the emerging lens.
the effective focal length $f$ is given by

$\frac{f_{1} | f_{2} |}{| f_{2} | - f_{1} + d}$

$\frac{f_{1} f_{2}}{f_{1} - f_{2} - d}$

$\frac{f_{1}}{f_{2} - f_{1} + d}$

$\frac{f_{2}}{f_{1} + f_{2} + d}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video, text & image solution for The following figure from shows version of a zoom.The converging lens has a focal length f_(1)and the diverging lens has focal length f_(2)=-|f_(2)|.the two lens are separated by a variable distance d that it is always less than f_(1),also the magnitude of the focal length of the diverging lens satisfies the inequality |f_(2)|gt(f_(1)-d). if the rays that emerge form the diverging lens and reach the final image point are extended backward to the left of the diverging lens,they will eventually expand to the original radius r_(o)at the same point.Q.To determine the effective focal length of the combination lens consider a bundle of parallel rays of radius r_(0)entering the emerging lens. the effective focal length f is given by by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS RAY OPTICS

Knowledge Check

The following figure from shows version of a zoom.The converging lens has a focal length $f_{1}$ and the diverging lens has focal length $f_{2} = - | f_{2} |$ .the two lens are separated by a variable distance d that it is always less than $f_{1},$ also the magnitude of the focal length of the diverging lens satisfies the inequality
$| f_{2} | > (f_{1} - d) .$

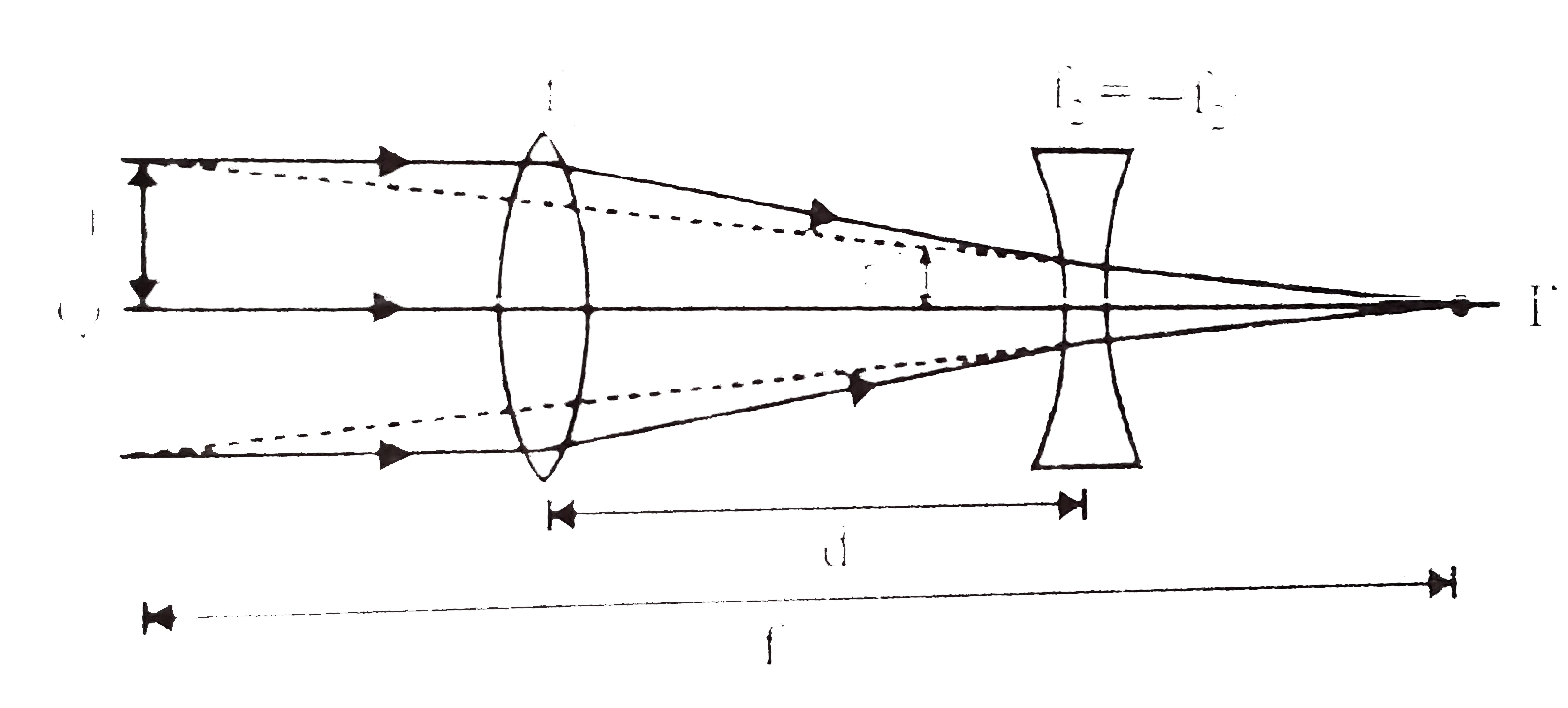
if the rays that emerge form the diverging lens and reach the final image point are extended backward to the left of the diverging lens,they will eventually expand to the original radius $r_{o}$ at the same point. $Q$ .To determine the effective focal length of the combination lens consider a bundle of parallel rays of radius $r_{0}$ entering the emerging lens.
To the right of the diverging lens the final image $I$ 'formed at a distance $S_{2}'$ given by
A $\frac{(f_{1} - f_{2}) d}{f_{1} - f_{2} + d}$
B $\frac{(f_{1} - d) f_{2}}{| f_{2} | + d - f_{1}}$
C $\frac{f_{1} - f_{2} + d}{f_{1} - f_{2}}$
D $\frac{(d - f_{1}) f_{2}}{f_{2} - f_{1} - d}$
The following figure from shows version of a zoom.The converging lens has a focal length $f_{1}$ and the diverging lens has focal length $f_{2} = - | f_{2} |$ .the two lens are separated by a variable distance d that it is always less than $f_{1},$ also the magnitude of the focal length of the diverging lens satisfies the inequality
$| f_{2} | > (f_{1} - d) .$

if the rays that emerge form the diverging lens and reach the final image point are extended backward to the left of the diverging lens,they will eventually expand to the original radius $r_{o}$ at the same point. $Q$ .To determine the effective focal length of the combination lens consider a bundle of parallel rays of radius $r_{0}$ entering the emerging lens.
AT the point where ray enters the diverging lens ,the radius of the ray bundle decreases to
A $r_{0}' = (\frac{f_{1} - d}{f_{1}}) r_{0}$
B $r_{0} = (\frac{f_{1} - d}{f_{1}}) r_{0}$
C $r_{0}' = (\frac{f_{1} - f_{2}}{f_{1}}) r_{0}$
D $r'_{0} = r_{0}$
The power (P) of a lens of focal length (f) is given by
AP = f
B $P = \frac{1}{f}$
C $P = - \frac{1}{f}$
D $P = - f$

The correct Answer is:A

Similar Questions

Knowledge Check

The power (P) of a lens of focal length (f) is given by

Recommended Questions