The figure shows a ray incident a angle i=π/3 of the plot drawn shown the variartion of |r−i|versusμ1μ2=k,(r=angle of refraction)

the value ofθ1
the value ofk1is2√3
the value ofθ1=π/6
the value ofθ2=π/3
the value ofk2is1
The correct Answer is:B,C,D
(B) at θ1 deviation is max so r=90∘=π/2
r−i=θ1⇒θ1=π/2−π/3⇒θ1=π6
(C ) at θ2 deviation is max.so r= 0
r−i=θ2⇒θ=π/3
(d) at k2deviation is 0 so μ1=μ2 therefore k2=1
Similar Questions
An equilateral prism of refractive index μ=4√3 is kept in a medium of refractive index μ1. Consider a light ray to be normally incident on one of the refracting faces. The diagram shows variation of magnitude of angle of deviation (β) with respect to μ1.
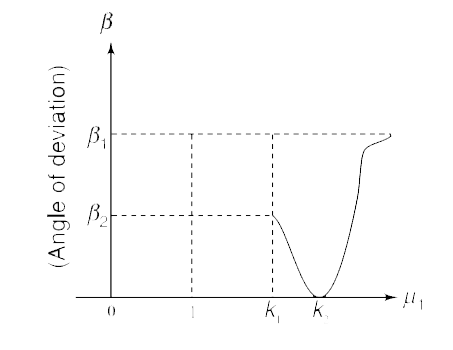
(a) Find value of k2.
(b) Find value of k1.
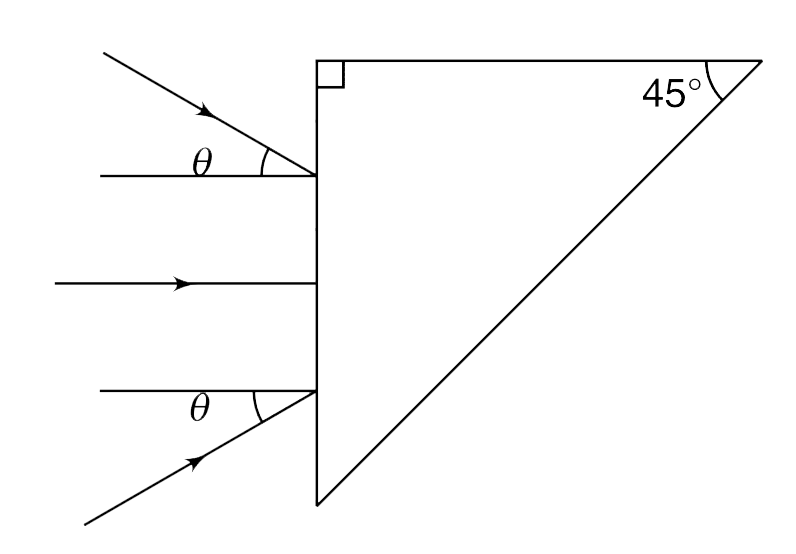
View SolutionA converging beam of light is incident on a right angled isosceles prism as shown in the Figure. The marginal rays in the beam are incident at angle ±θ. The refractive index for the glass of the prism is μ=1.49(=1sin42°) . Find the maximum value of θ for which no light comes out of the hypotenuse surface.
View Solution
Knowledge Check
The figure shows a ray incident a angle i=π/3 of the plot drawn shown the variartion of |r−i|versusμ1μ2=k,(r=angle of refraction)

the value ofk1isA2√3B1C1√3D√32The figure shows a ray incident a angle i=π/3 of the plot drawn shown the variartion of |r−i|versusμ1μ2=k,(r=angle of refraction)

the value of k2 isA1B2C1/2DnoneWhen a monochromatic light ray is incident on a medium of refracive indexμwith angle of incidence θ1,the angle of refraction is θr.if θi is changed slightly byΔθi,then the corresponding change in θrwill be-
AΔΘiBμΔθiC1μ.cosθ1cosθr.ΔθiDμ.sinθ1sinθr.Δθi
A monochromatic light is incident on the plane interface AB between two media of refractive indices μ1 and (μ2>μ1) at an angle of incidence θ as shown in Fig.
The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive index μ3 is introduced on the interface (as shown in the figure), show that for any value of μ3 all light will ultimately be reflected back into medium II.

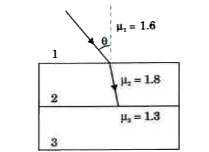
View SolutionA ray of light refracts from medium 1 into a thin layer of medium 2, crosses the layer and is incident at the critical angle on the interface between the medium 2 and 3 as shown in the figure. If the angle of incidence of ray is θ, the values of θ is
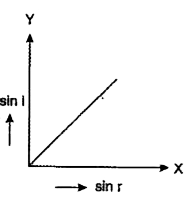
View SolutionWhen a ray of light undergoes refraction, a straight line graph is obtained by plotting sine of angle of incidence versus sine of angle of refraction. The slope of this graph represents.
View SolutionRead the paragraph and the figure carefully and answer the questions.

The figure shows a constant deviation prism ABCD. The incident ray is PQ and the emergent ray is ST. Although it is made up of one piece of glass, it is equivalent to two 30∘−60∘−90∘ prisms and one 45∘−45−90∘ prism. The angle θ1 is the angle of incidence on face AB. The path of the ray inside the prism is indicated in the figure.
For this prism, μ=2sinθ1
The angle of refraction on the face AB is
View SolutionA ray of light, travelling in a medium of refractive index mu, is incident at an angle i on a composite transparent plate consisting of three plates of refractive indices μ1,μ2andμ3. The ray emerges from the composite plate into a medium of refractive index μ4, at angle x. Then,
View Solution
