A rod AB of mass and length L is lying on a horizontal frictionless surface. A particle of mass travelling along the surface hits the end A of the rod with a velocity in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time after the collision.
The correct Answer is:(a) ;
(b) ;
( c)
Let just after collision, velocity of of rod is and angular velocity about is .
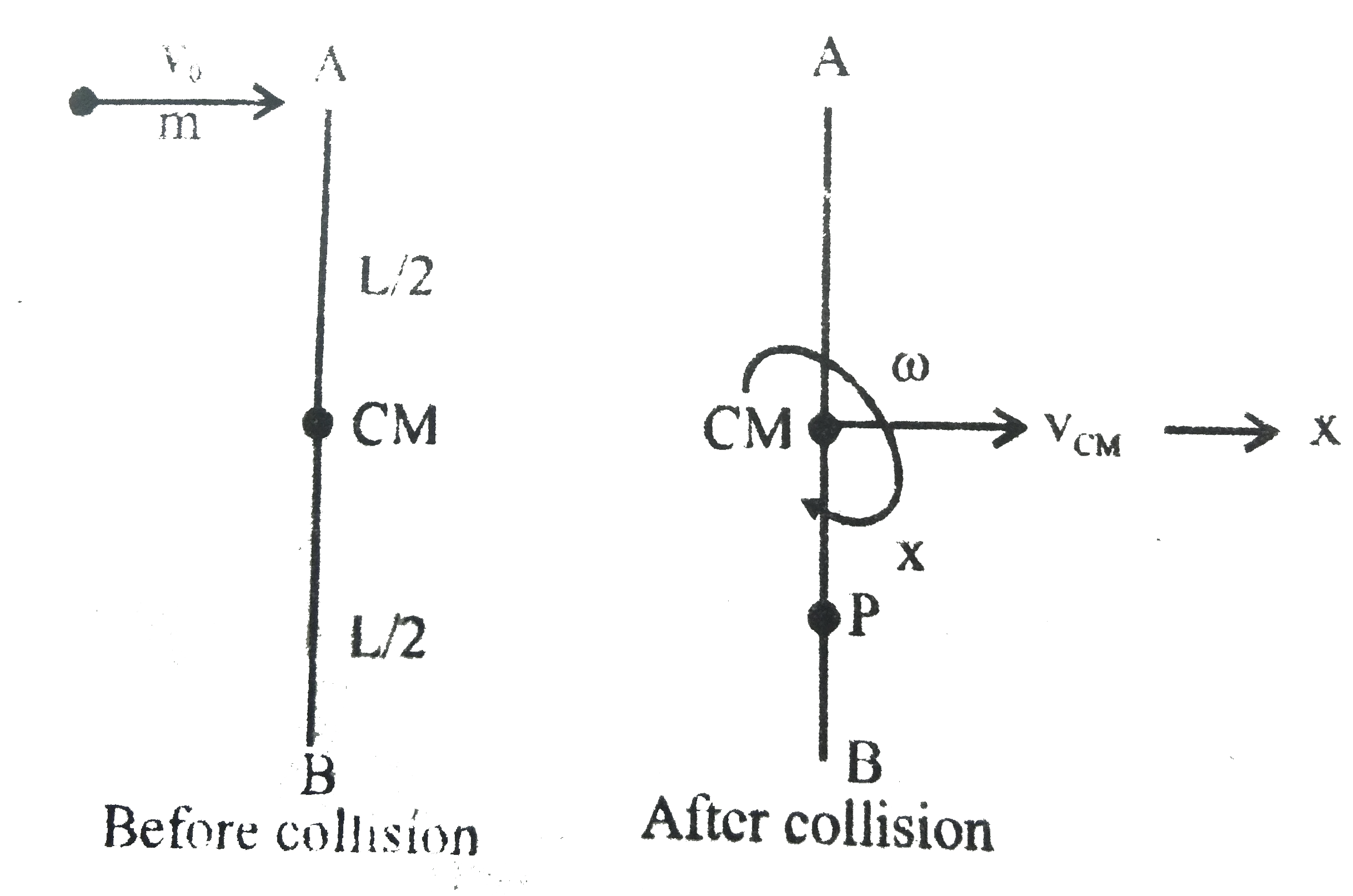
from conservation of linear momentum in
….(1)
from conservation of angular momentum about of rod
....(2)
since, the collision is elastic kineticenergyis alos conserved.
...(3)
From equation (1),(2) and (3)
and
(b) Point will be at rest if
( c) 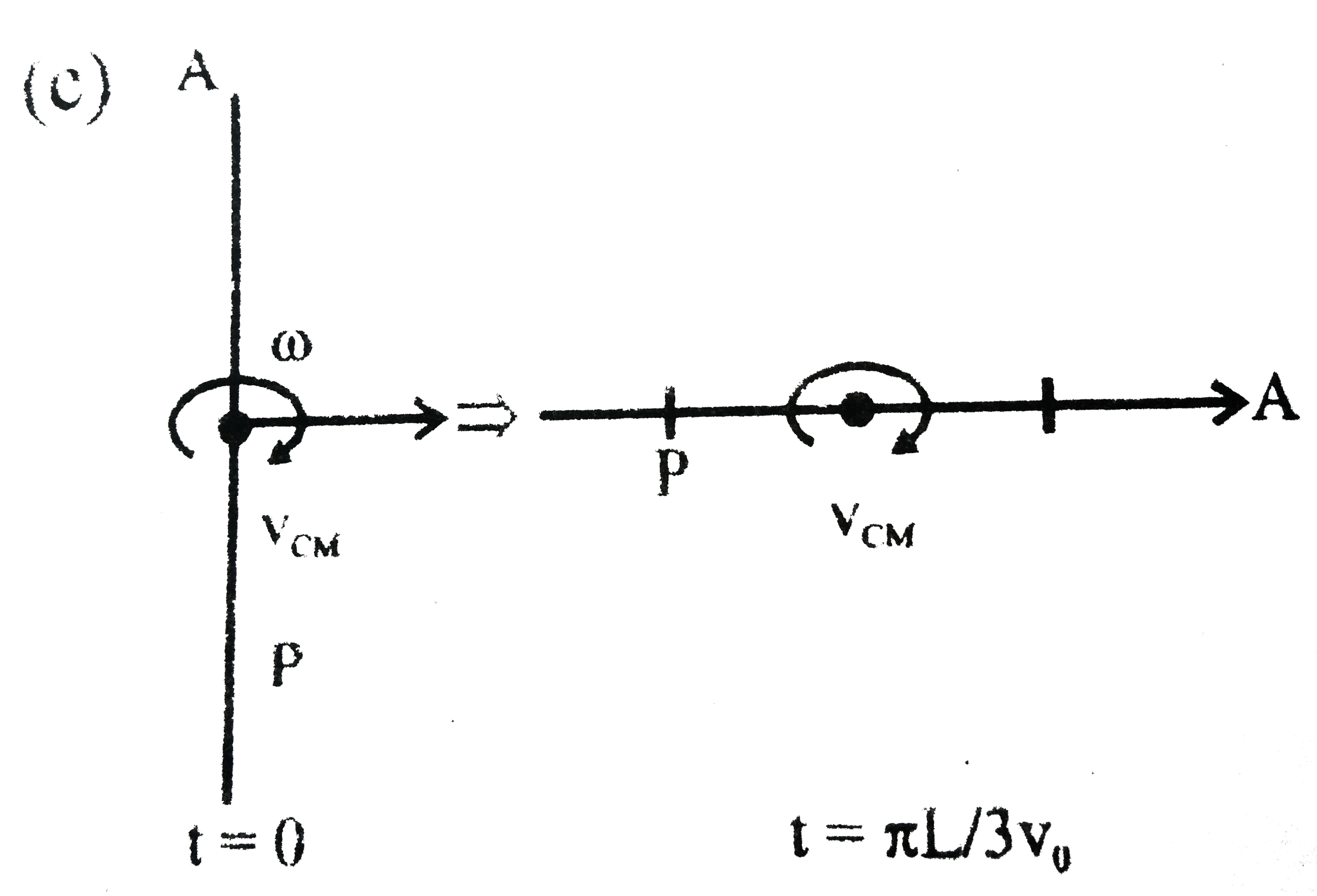
after time
angle rotated by rod
put
resultant velocity of point will be
.
Similar Questions
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with a velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses (mM) is 1x. The value of 'x' will be_____.
View Solution
Knowledge Check
A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0A rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37∘ with the rod. The collision is elastic. After collision,
 Athe angular velocity of the rod will be 72/55v/lBthe centre of the rod will travel a distance it πl/3 in the time in which it makes half rotationCimpulse of the impact force is 24mV/55Dnone of these
Athe angular velocity of the rod will be 72/55v/lBthe centre of the rod will travel a distance it πl/3 in the time in which it makes half rotationCimpulse of the impact force is 24mV/55Dnone of these
A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
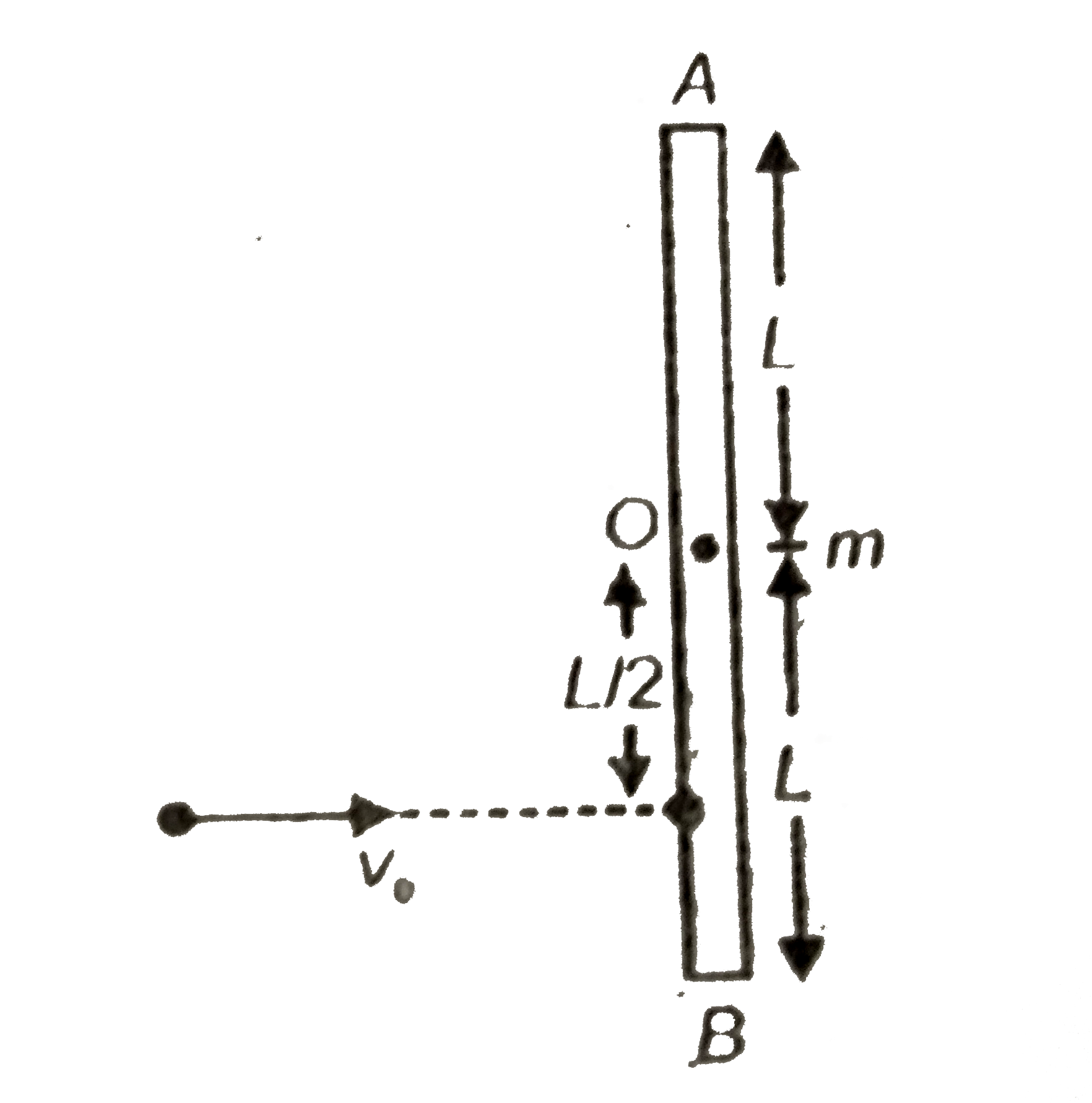
Angular velocity of rod just after collision is
View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
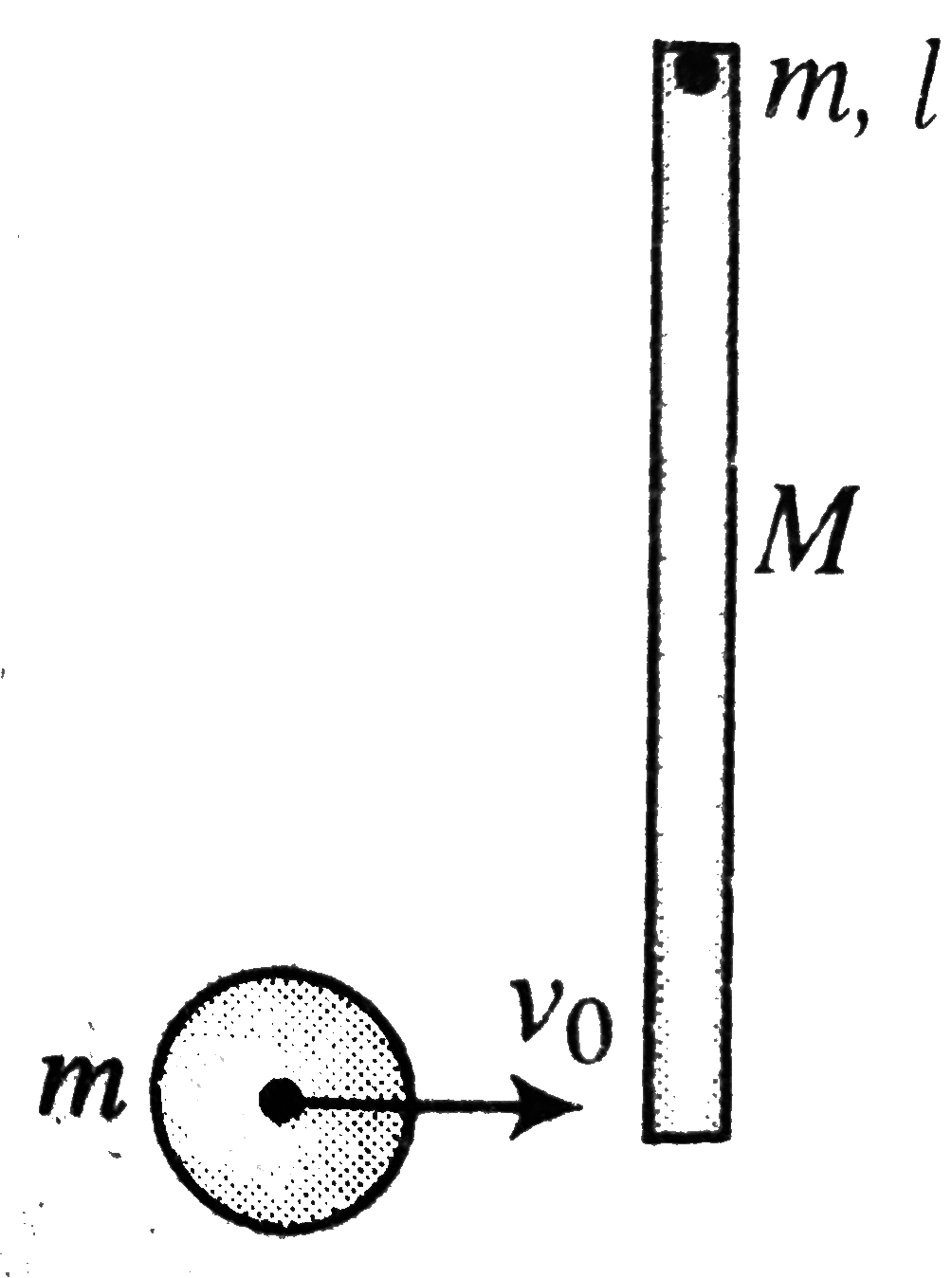
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
View Solution
