A thin wire of length $L$ and uniform linear mass density $ρ$ is bent into a circular loop with centre at $O$ as shown. The moment of inertia of the loop about the axis $X X'$ is :
.

A

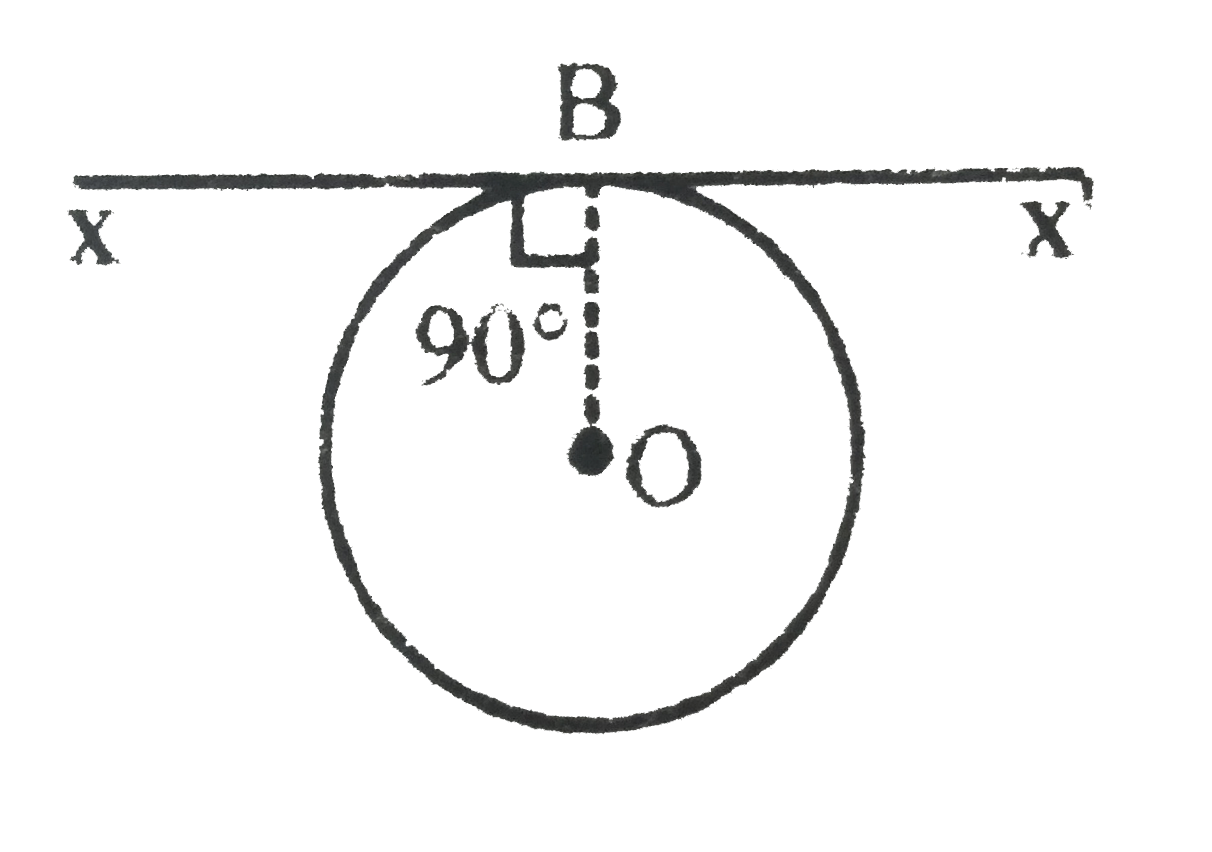$ρ L^{3} / 8 π^{2}$

B

$ρ L^{3} / 16 π^{2}$

C

$5 ρ L^{3} / 16 π^{2}$

D

$3 ρ L^{3} / 8 π^{2}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

From parallel axis theorem
$I_{\times'} = I_{0} + M R^{2} \Rightarrow I_{\times'} = \frac{1}{2} M R^{2} + M R^{2}$
$I_{\times'} = \frac{3}{2} M R^{2}$
$I_{\times'} = \frac{3}{2} ρ \times L \times {(\frac{L}{2 π})}^{2} \Rightarrow I_{\times'} = \frac{3}{8} \frac{ρ L^{3}}{8 π^{2}}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
A thin wire of length L and uniform linear mass density p is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is

A $\frac{p L^{3}}{8 π^{2}}$
B $\frac{p L^{3}}{16 π^{2}}$
C $\frac{5 p L^{3}}{16 π^{2}}$
D $\frac{3 p L^{3}}{8 π^{2}}$
Question 2 - Select One
A thin wire of length L and uniform linear mass density $ρ$ is bent into a circular loop with centre at O as shown in the figure. What is the moment of inertia of the loop anout the axis XX'?
A $\frac{ρ L^{3}}{16 π^{2}}$
B $\frac{ρ L^{2}}{8 π^{2}}$
C $\frac{5}{16} ρ L^{3} π$
D $\frac{3 ρ L^{3}}{8 π^{2}}$
Question 3 - Select One
A thin wire of length $L$ and uniform linear mass density $ρ$ is bent into a circular loop with centre at $O$ as shown. The moment of inertia of the loop about the axis $X X'$ is :
.
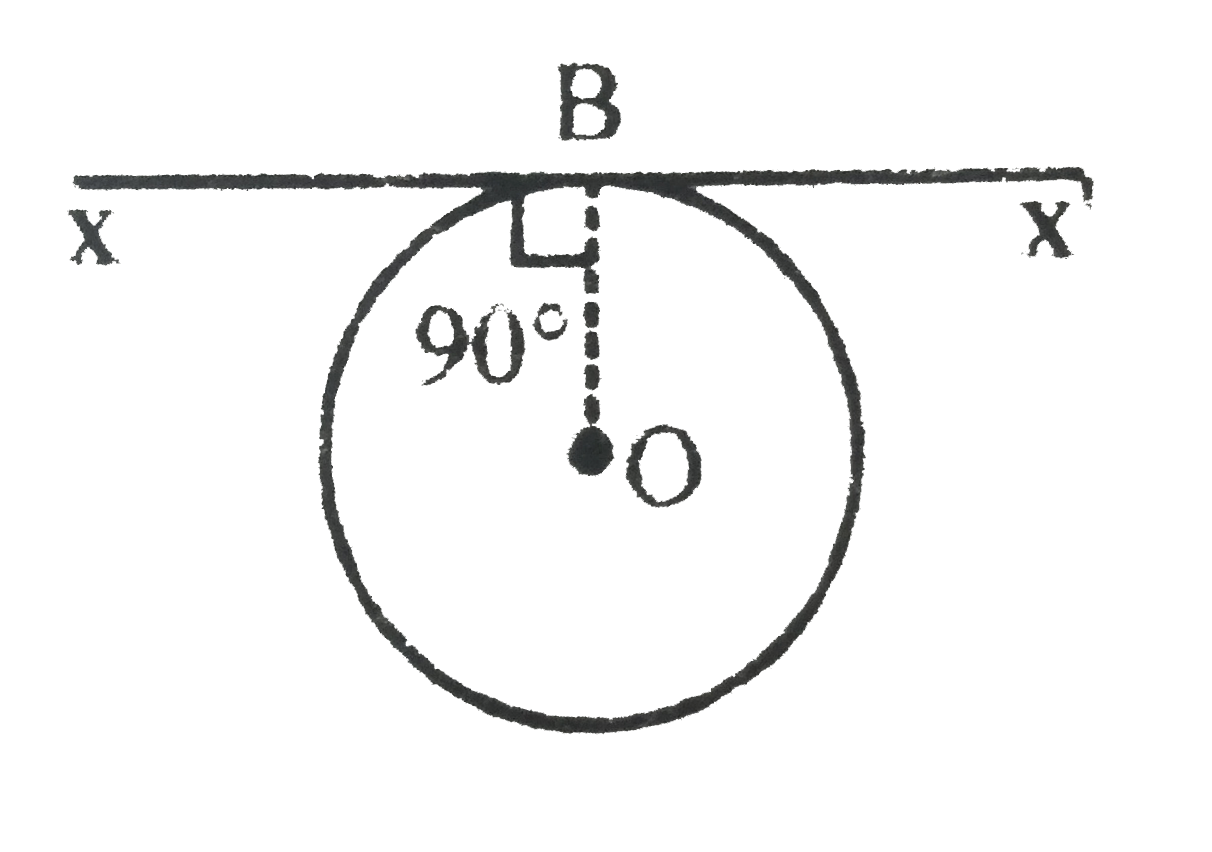A $\frac{3 ρ L^{2}}{8 π^{2}}$
B $\frac{8 π^{2}}{3 ρ L^{3}}$
C $\frac{3 ρ L^{3}}{8 π^{2}}$
D $\frac{8 π^{2}}{3 ρ L^{2}}$

Recommended Questions

Home
Ask Doubt
Profile