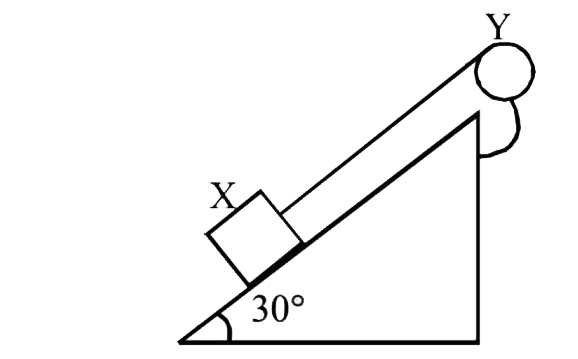
A block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2 and of radius 0.2 m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s calculate the distance travelled by X from that instant of time until it comes to rest
The correct Answer is:
(a) Let a be the linear retardation of block and is the angular retardation of drum . Then, is the angular retardation of drum . Then,
….(1)
….(2)
or ...(3)
solving Eqs. (1),(2) and (3) for , we get
substituting the value, we get
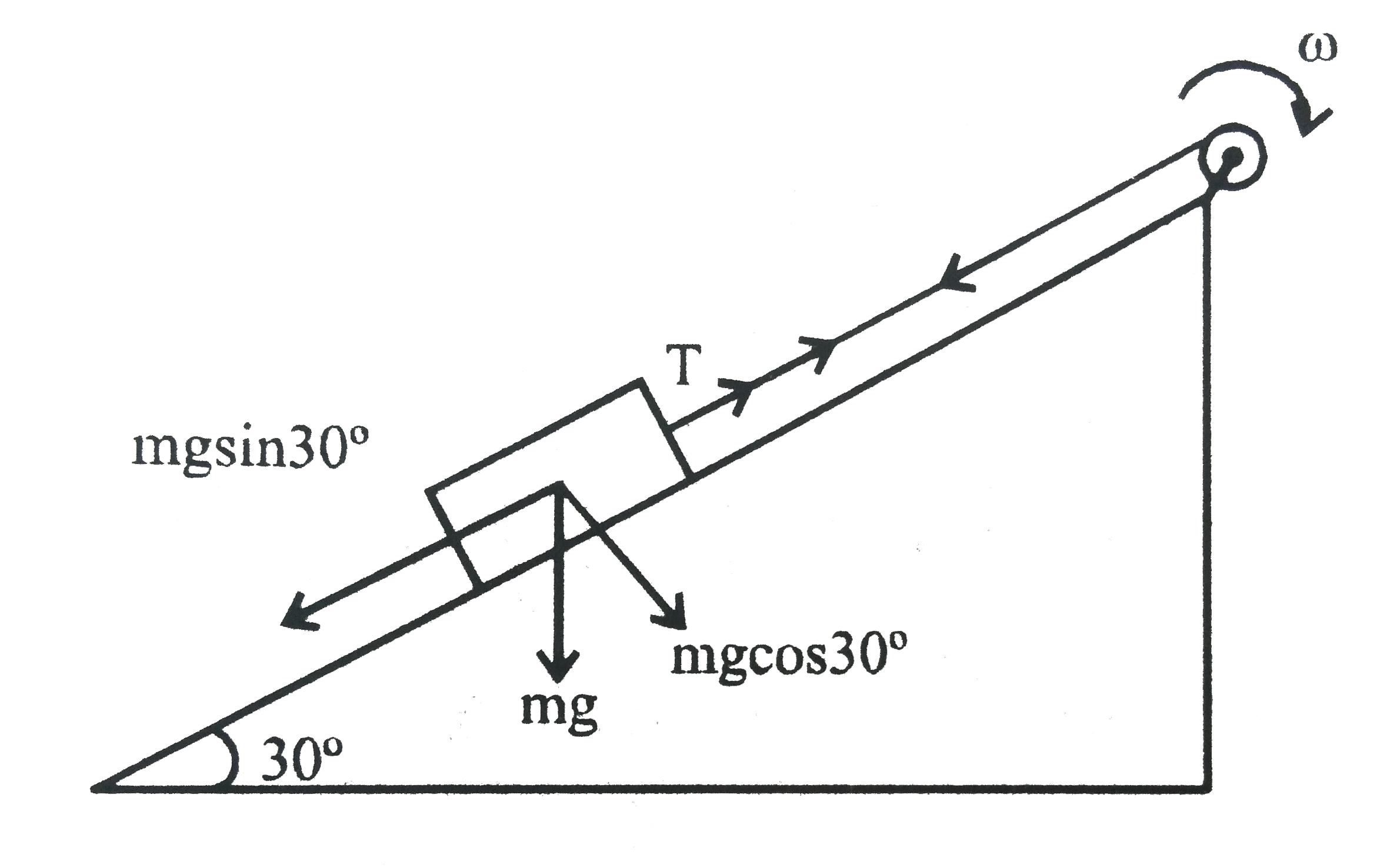
(ii) From Equation (3), angular retardation of drum
or linear retardation of block
At the moment when angular velocity of drum is
The linear velocity of block will be
Now, the distance (s) travelled by the block until it comes to rest will be given by
or .
Similar Questions
A block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is

View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View Solution
Knowledge Check
A block of mass 10kg is pushed up on a smooth incline plane of inclination 30∘, so that it has acceleration 2m/s2. The applied force is
A50 NB60 NC70 ND80 NA person pushes a block of mass 4 kg up a frictionless inclined plane 10 m long and that makes an angle of 30∘ with the horizontal . Then the work done is
A33.5JB−392JC339.4JD−196JA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ
A ring of mass 1kg and radius 1m is moving with a velocity of 1m/s by rolling on a frictionless inclined plane. The total kinetic energy of the ring is
View SolutionA block of mass 10 kg rests on a rough inclined plane of inclination 45∘ with the horizontal. What minimum force is required to just move the block up the inclined plane. Given μs=0.5andg=10ms−2.
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
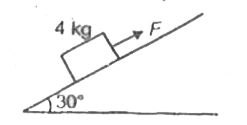
View SolutionA block of mass 10 kg is placed on an inclined plane when the angle of inclination is 30∘. The block just begins to slide down the plane. The force of static friction is
View SolutionA block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
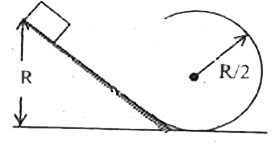
View Solution
