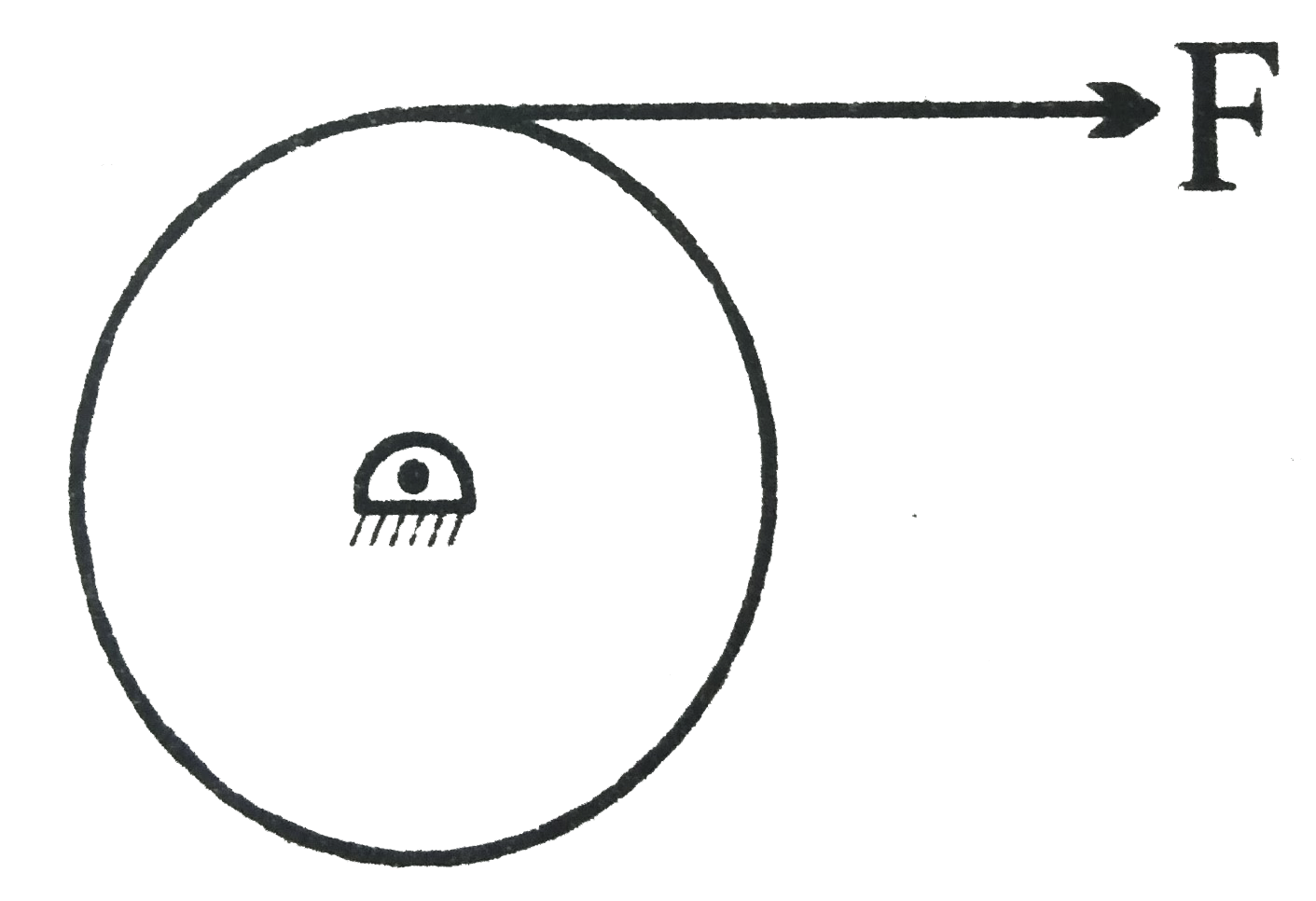
A pulley is hinged at the centre and a massless thread is wrapped around it. The thread is pulled with a contant froce starting from rest. As the time increases -
 .
.
Its angular velocity increases, but force on hinge remains constant
its angular velocity remains same, but force on hinge increases.
its angular velocity increases and force on hinge increases
its angular velocity remains same and force on hinge is constant.
The correct Answer is:A
Due to torque provided by force pulley will have angular acceleration and its's angular velocity increase. Force on hinge is always equal and opposite to .
Similar Questions
A spool has a mass of 2 kg,an inner radius R1 =3cm,and an outer radius R2=5cm, the radius of gyration about the axis of the spool is if=4cm.A constant horizontal force of 5N is applied to the free end of a massless thread that is wrapped around the inner cylinder of the spool as shownin figure-5.150. If the spool rolls without slipping, calculate the linear acceleration along the horizontal surface. What is the minimum coefficient of static friction required to prevent slipping ?

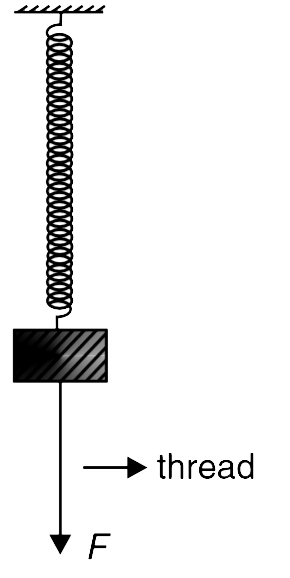
View SolutionA vertical spring supports a block in equilibrium. The spring is designed to break when extension in it crosses a limit. There is a light thread attached to the block as shown. The thread is pulled down with a force F which gradually increases from zero. The spring breaks when the force becomes F0. Instead of gradually increasing the force, if the thread were pulled by applying a constant force, for what minimum value of the constant force the spring will break?
View Solution
Knowledge Check
Three masses M1,M2 and M3 are lying on a frictionless table. The masses are connected by massless threads as shown. The mass M3 is pulled by a constant force F as shown. The tension in the thread between masses M2 and M3 is
 A(M1+M2M1+M2+M3)FB(M2+M3M1+M2+M3)FC(M1+M3M1+M2+M3)FD(M1+M2M1+M2+M3)F
A(M1+M2M1+M2+M3)FB(M2+M3M1+M2+M3)FC(M1+M3M1+M2+M3)FD(M1+M2M1+M2+M3)FThe intial configuration of the system is as shown in the figure.
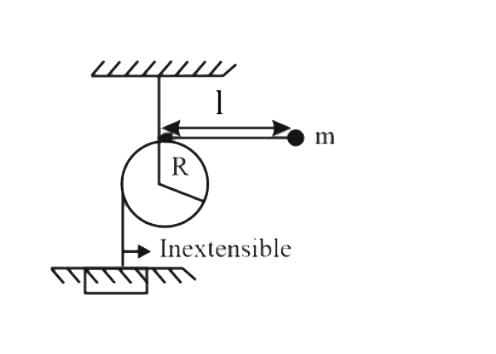
The string and the pulley are light. The bob is released and the string starts wrapping around the pulley. (The pulley is held in place by a force applied at the centre)

Find the rate r at which the length of the string warpped around the pulley increaes (as a function of θ).Ar=R(l−Rθ)√[2g(l−Rθ)sinθ]Br=R(l−Rθ)√2g[(l−Rθ)sinθ+Rcosθ]Cr=R(l−Rθ)√2g[(l−Rθ)sinθ+R(1−sinθ)]Dr=R)(l−Rθ)√2g[(l−Rθ)sinθ+R(1−cosθ)]A rod is hinged at its centre and rotated by applying a constant torque starting from rest. The power developed by the external torque as a function of time is :
A B
B C
C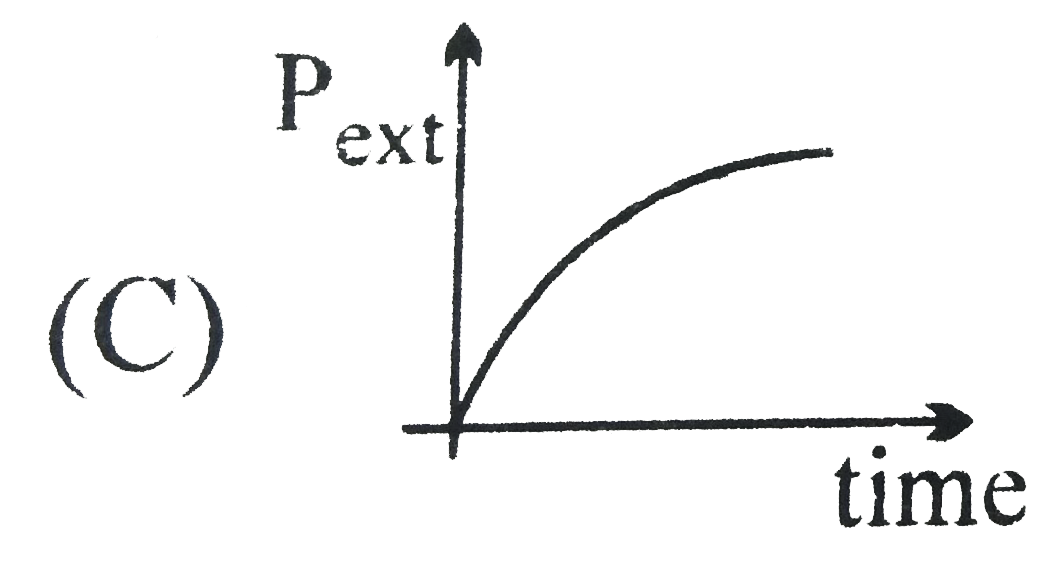 D
D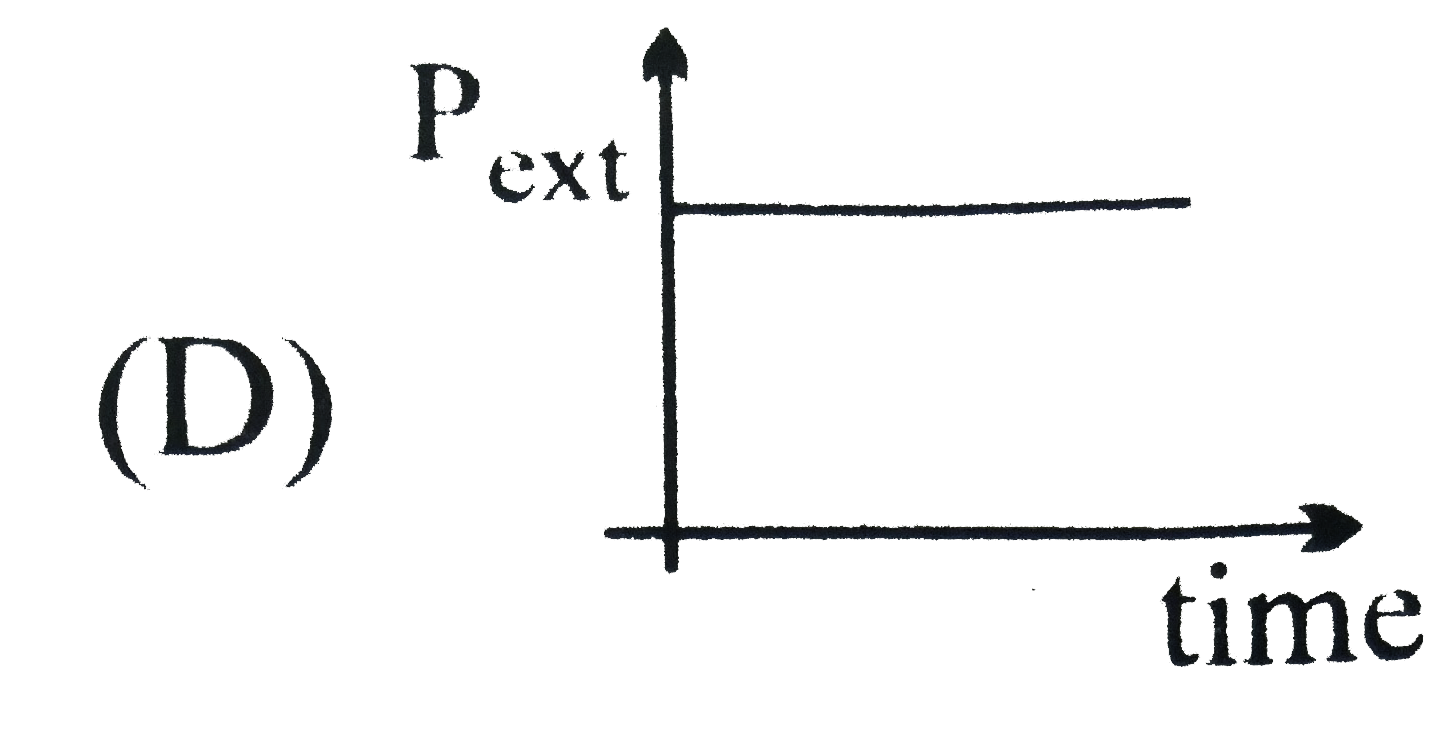
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F(figure).
Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k. What is the acceleration wmax of the axis of the cylinder rolling down the inclined plane?

View SolutionA very long non-conducting cylindrical shell of length l=10m is free of rotate about its fixed axis. A light inextensible thread is wrapped over non-conducting cylindrical surface and one end P is pulled with constant acceleration of F2m.F is the force applied at P and m is the mass of cylinder. Then charge on the cylinder will be 5×10K coulomb. [Given m=25kg,l=10m]. Find the value of K?

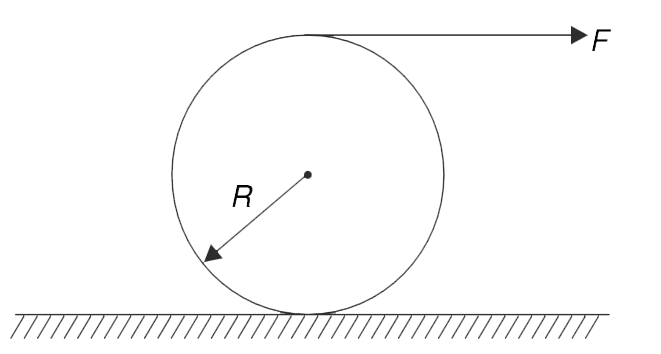
View SolutionLight thread is tightly wound on a uniform solid cylinder of radius R. The cylinder is placed on a smooth horizontal table and the thread is pulled horizontally as shown, by applying a constant force F. How much length of the thread is unwound from the cylinder by the time its kinetic energy becomes equal to K.
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
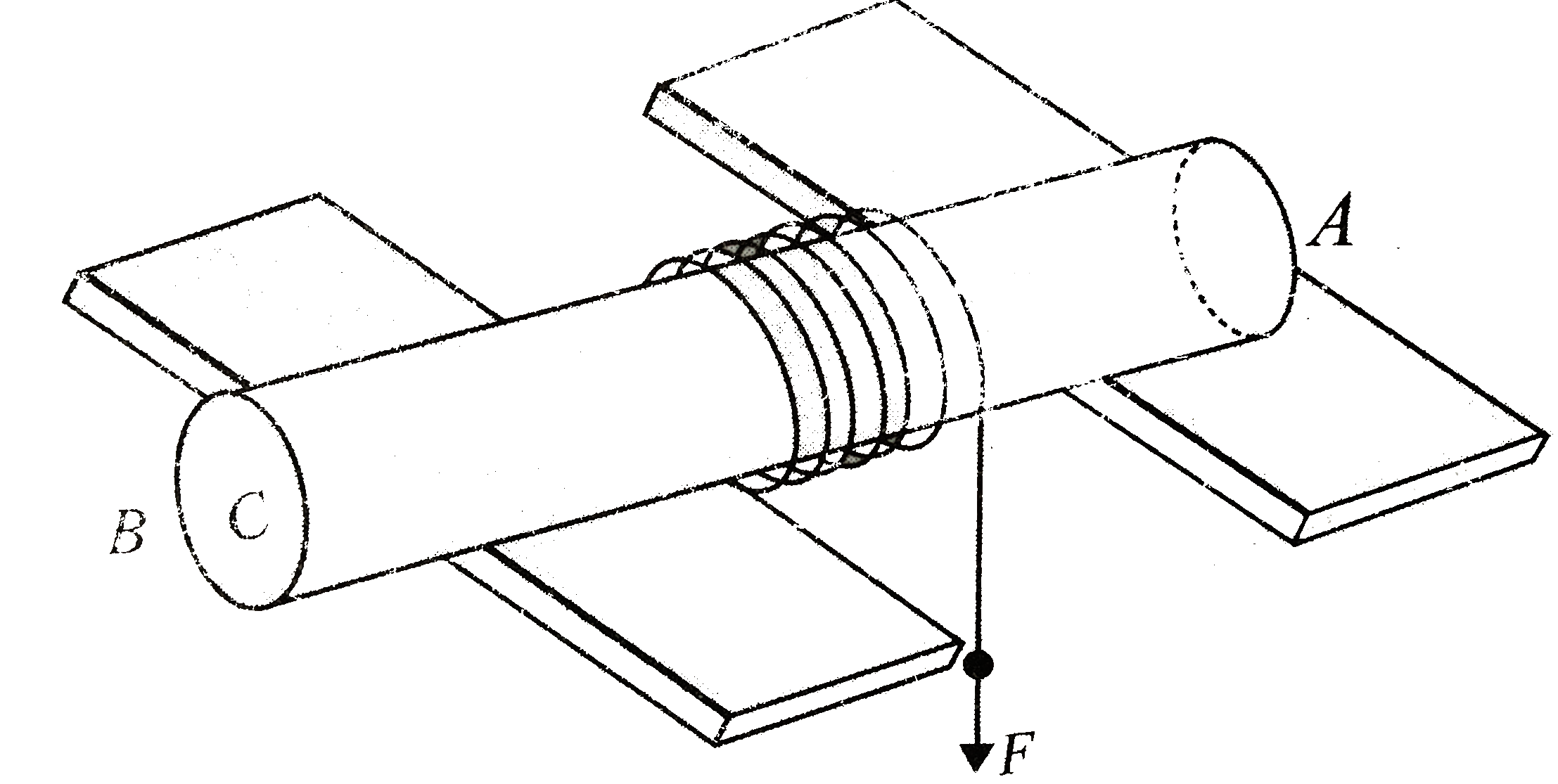
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionConsider a perfectly conducting uniform disc of mass m and radius 'a' hinged in a vertical plane from its centre and free to rotate with respect to hinge. A resistance R is connected between centre of the disc annd periphery by using two sliding contacts C1 & C2. A long non -conducting massless string is wrapped around the disk, whose another end is attached with a block of mass m. There exists a uniform horizontal magnetic field B, whose arrangement is shown in figure.

Given system is released from rest at t=0. Assume friction between string and disc is sufficient so that there is no slipping between them let at any instant t, velocity of block is v, angular velocity of the disc is ω and current in resitance is i
Find the terminal speed of the block of mass m (Terminal speed = constant speed attained by the block after very long time)
View Solution
