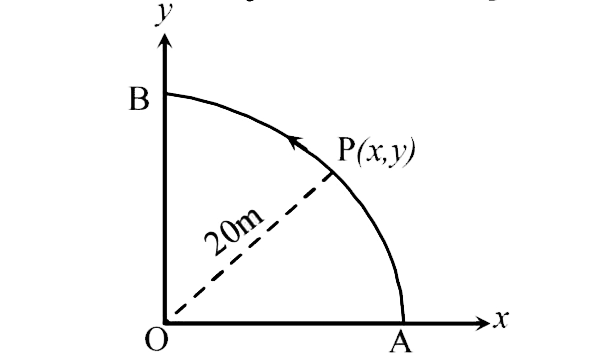
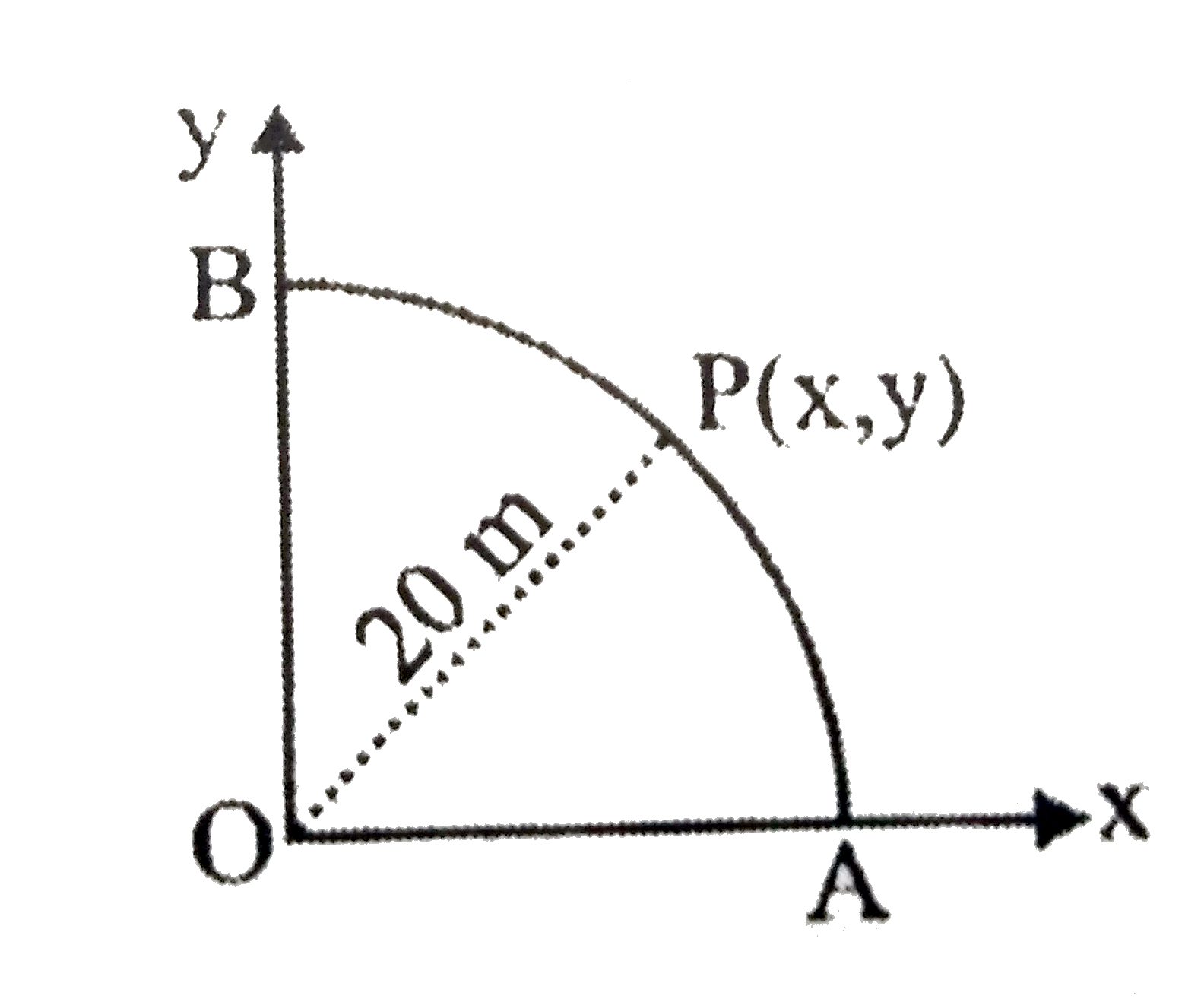
A point p moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length s=t3+5 , where s is in metres and t is in seconds . The radius of the path is 20m . The acceleration of 'P' when t=2s is nearly .
14m/s2
13m/s2
12m/s2
7.2m/s2
The correct Answer is:A
S=t3+5
Linear speed of the particle
v=dSdt=3t2
at t=2sv=(3×2)m/s
12m/s
Linear acceleration
a1=dvdt=6t
at t=2s,a1=12m/s2
The centripetal acceleration
a2=v2R=12220m/s2
=7.2m/s2
∴a≠t=√a21+a22=√122+7.22=14m/s2
Similar Questions
A point P moves in counter-clockwise direction on figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in metre and t is in second. The radius of the pathh is 20 m. the acceleration of P when t=2s is nearly
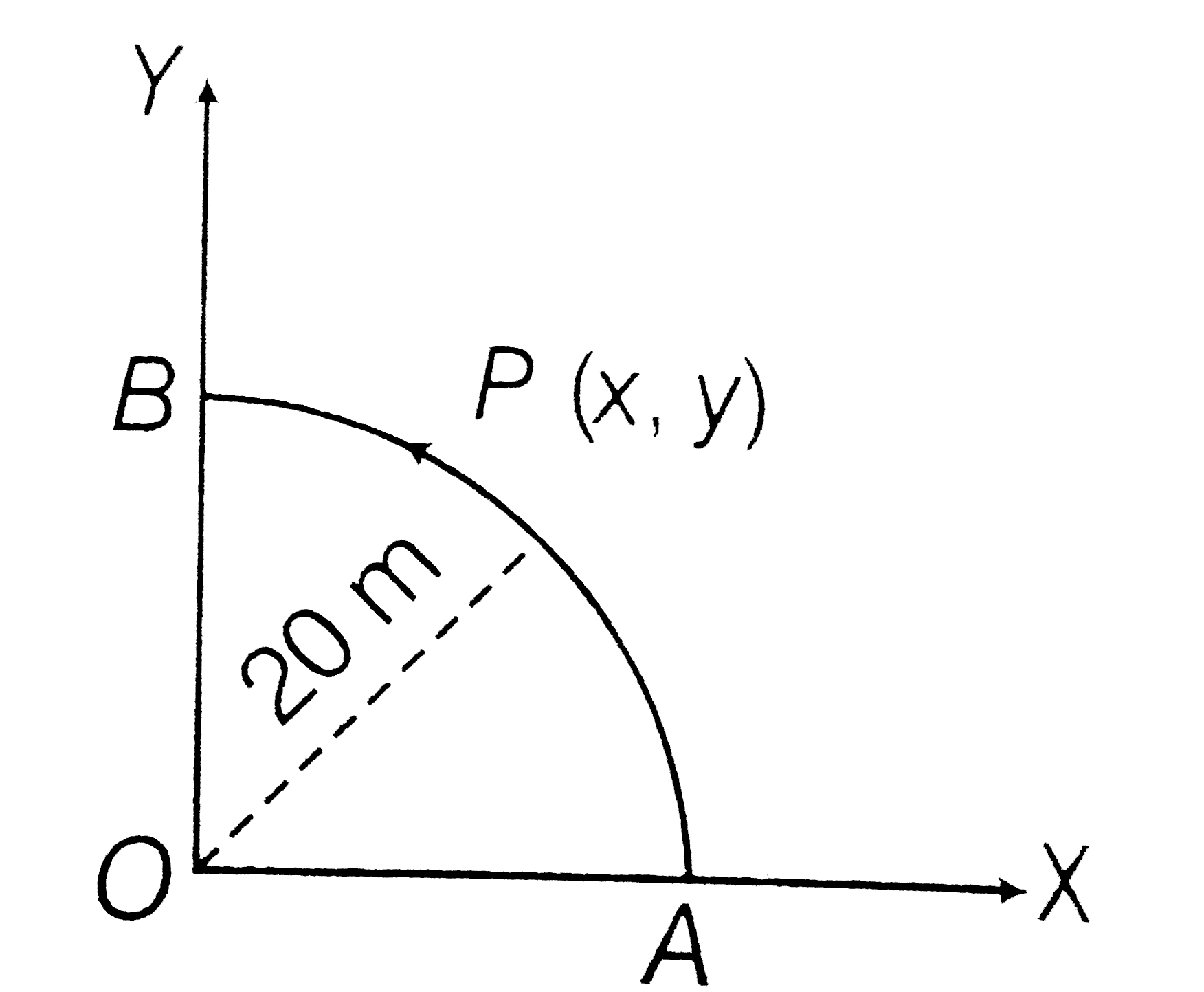
View SolutionA point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of P when t = 2 s is nearly
View Solution
Knowledge Check
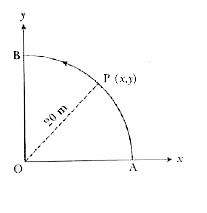
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5, where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of P when t = 2 s is nearly
 A14m/s2B13m/s2C12m/s2D7.2m/s2
A14m/s2B13m/s2C12m/s2D7.2m/s2A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P ' is such that it sweeps out a length s=t3+5 where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of ' P ' when t = 2 s is nearly:
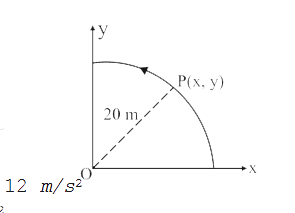 A13m/s2B12m/s2C7.2m/s2D14m/s2
A13m/s2B12m/s2C7.2m/s2D14m/s2A point P moves in counter clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length s=t2+5, wheres is in metres and t is in seconds. The radius of the path is 20m. The acceleration of 'P' when t=5√310 seconds is nearly:
 A2m/s2B1.5m/s2C2.5m/s2D3m/s2
A2m/s2B1.5m/s2C2.5m/s2D3m/s2
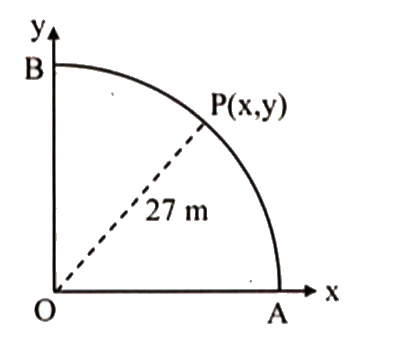
A point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5 where s is in the metre and t is in seconds. The radius of the path is 27 m. The acceleration of P when t= 3 s is _________ m/s2. (Take √13=3.6)
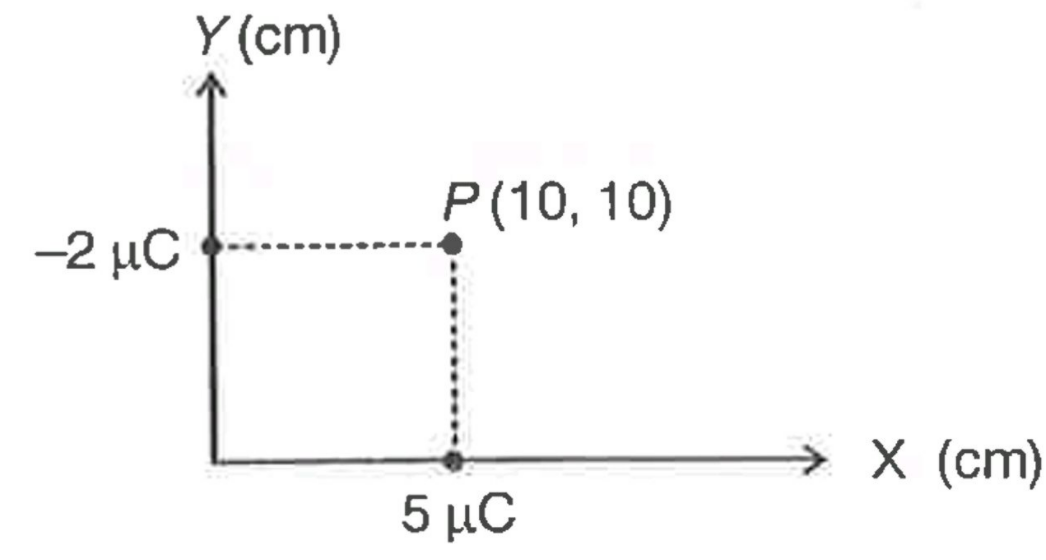
View SolutionTwo charges are placed s shown in figure below. The potential at point P is
View SolutionA point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5 where s is in the metre and t is in seconds. The radius of the path is 27 m. The acceleration of P when t= 3 s is _________ m/s2. (Take √13=3.6)

View SolutionThe displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
View SolutionA car moves along a straight line whose equation of motion is given by
s=12t+3t2−2t3
where s is in metres and t is in seconds. The velocity of the car at start will be :-
View Solution
