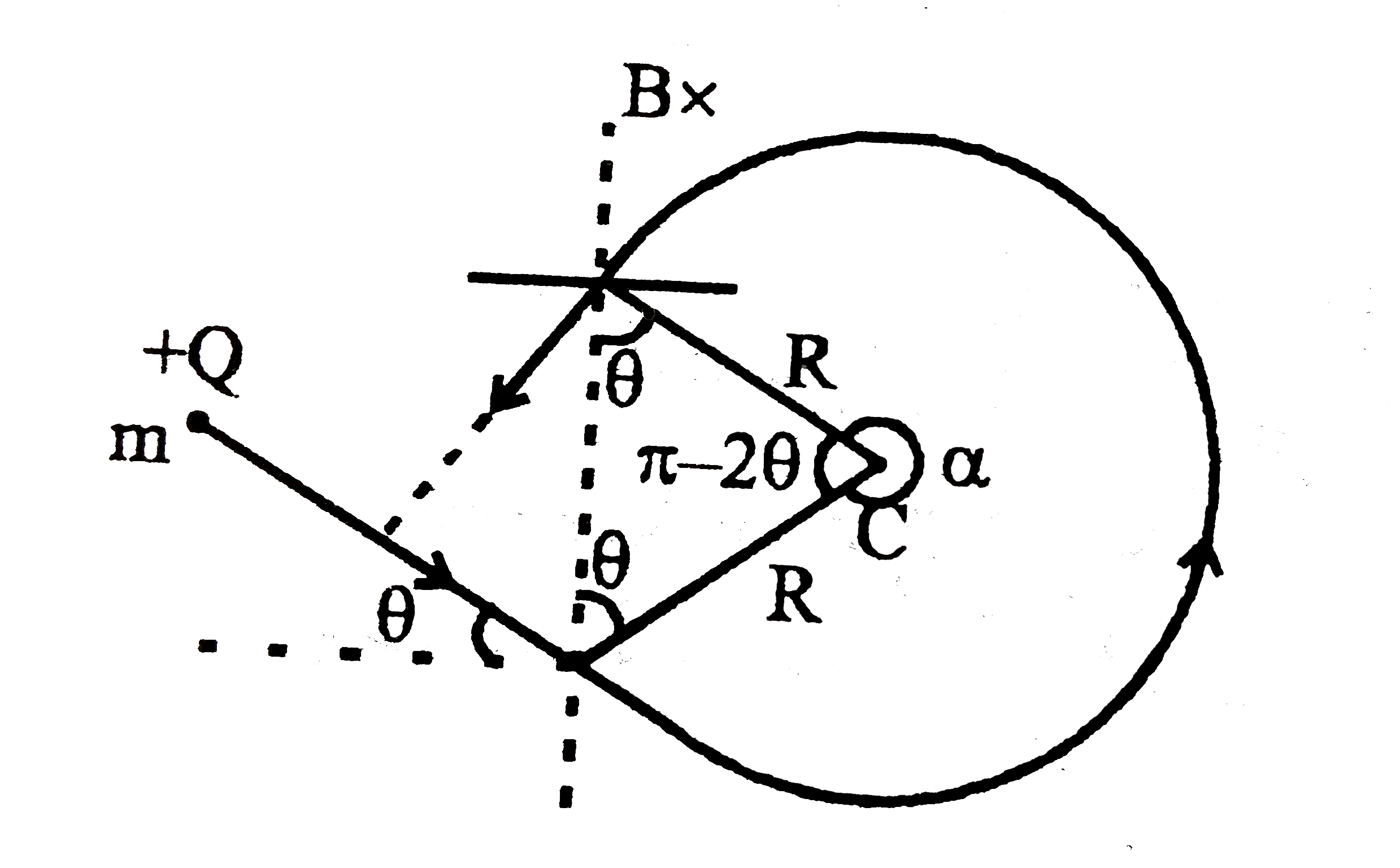
A particle with charge +Q and mass m enters a magnetic field to magnit

A charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle $θ$ with the field. The frequency of revolution of the particle
ADepends on the angle $θ$
BIs independent of the angle $θ$
CIs proportional to the specific charge q/m of the particle
DIs inversely proportional to the value of B
Positively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
AAccelerated
BDecelerated
CDeflected
DNo change in velocity
A charged particle enters into a magnetic field with velocity vector making an angle of $30^{\circ}$ with respect of the direction of magnetic field. The path of the particle is
Acircular
Bhelical
Celliptical
Dstraight line

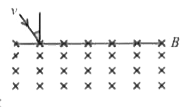
A particle with charge $+ Q$ and mass m enters a magnetic field to magnitude $B$ existing only of the right of the boundary $Y Z$ The direction of the motion of the particle is perpendicular to the direction of $B$ Let $T = 2 π \frac{m}{Q B}$ The time spent by the particle in the field will be
.