A rod of length L and cross-section area A lies along the x-axis between x=0 and x=L. The material obeys Ohm's law and its resistivity varies along the rod according to ρ(x)=ρ0ε−x/L. The end of the rod x=0 is at a potential V0 and it is zero at x=L.
(a) Find the total resistance of the rod and the current in the wire.
(b) Find the electric potential in the rod as a function of x.
The correct Answer is:R=ρ0LA(1−1e);I=V0Aρ0L(ee−1);V=V0(e−x/L−e−1)1−e−1
(a) For Resistance
dR=ρdxA
R=∫L0ρ0e−x/LdxA=ρ0A∫L0e−x/Ldx
=ρ0A[−Le−x/L]L0=ρ0AL[1−e1]
R=ρ0AL(1−1e)
For current
I=V0−0R⇒I=V0R⇒I=VoAρ0L(ee−1)
(b) For potential at any point
V=V0−IR
V=V0−V0Aρ0L(11−e−1)×∫x0dR
V=V0−V0Aρ0L(1−e−1)×ρ0A∫x0e−x/Ldx
V=V0(e−x/L−1)1−e−1
Similar Questions
A rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is λ such that λ=a+bx. Find the mass of the rod.
View SolutionA rod of length L and cross-section area A lies along the x-axis between x=0 and x=L. The material obeys Ohm's law and its resistivity varies along the rod according to ρ(x)=ρ0ε−x/L. The end of the rod x=0 is at a potential V0 and it is zero at x=L.
(a) Find the total resistance of the rod and the current in the wire.
(b) Find the electric potential in the rod as a function of x.
View Solution
Knowledge Check
A rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
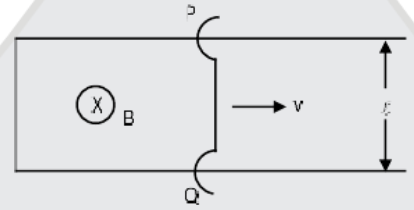 A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)
A(12)(BvlR)B(2BvlR)C(3BvlR)D(BvlR)A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLA conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
ABlvRBBlvCzeroDB2v2l2R
A rod of length L is placed along the X-axis between x=0andx=L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρj=a+bx. a. Find the SI units of a and b. b. Find the mass of the rod in terms of a,b, and L.
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/ length) λ of the rod varies with the distance x from the origin as λ=Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/length) λ of the rod varies with the distance x from the origin as λ = Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
