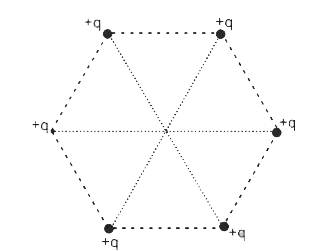
Six charges are placed at the vertices of a rectangular hexagon as shown in the figure. The electric field on the line passing through point O and perpendicular to the plane of the figure as a function of distance x from point O is (xgtgta)

The correct Answer is:0
We can consider charges of AD,EB,CF as a diple . Now the line passing through O and perpendicular to the plane will act like an equitorial line .
Let point P at distance x from O. Field at P will be vector sum of field due to three dipoles
→EP=→EAD+→EBF_→ECF
EP=0
(##NG_PHY_C01_E01_120_S02.png" width="80%">.
Similar Questions
Knowledge Check
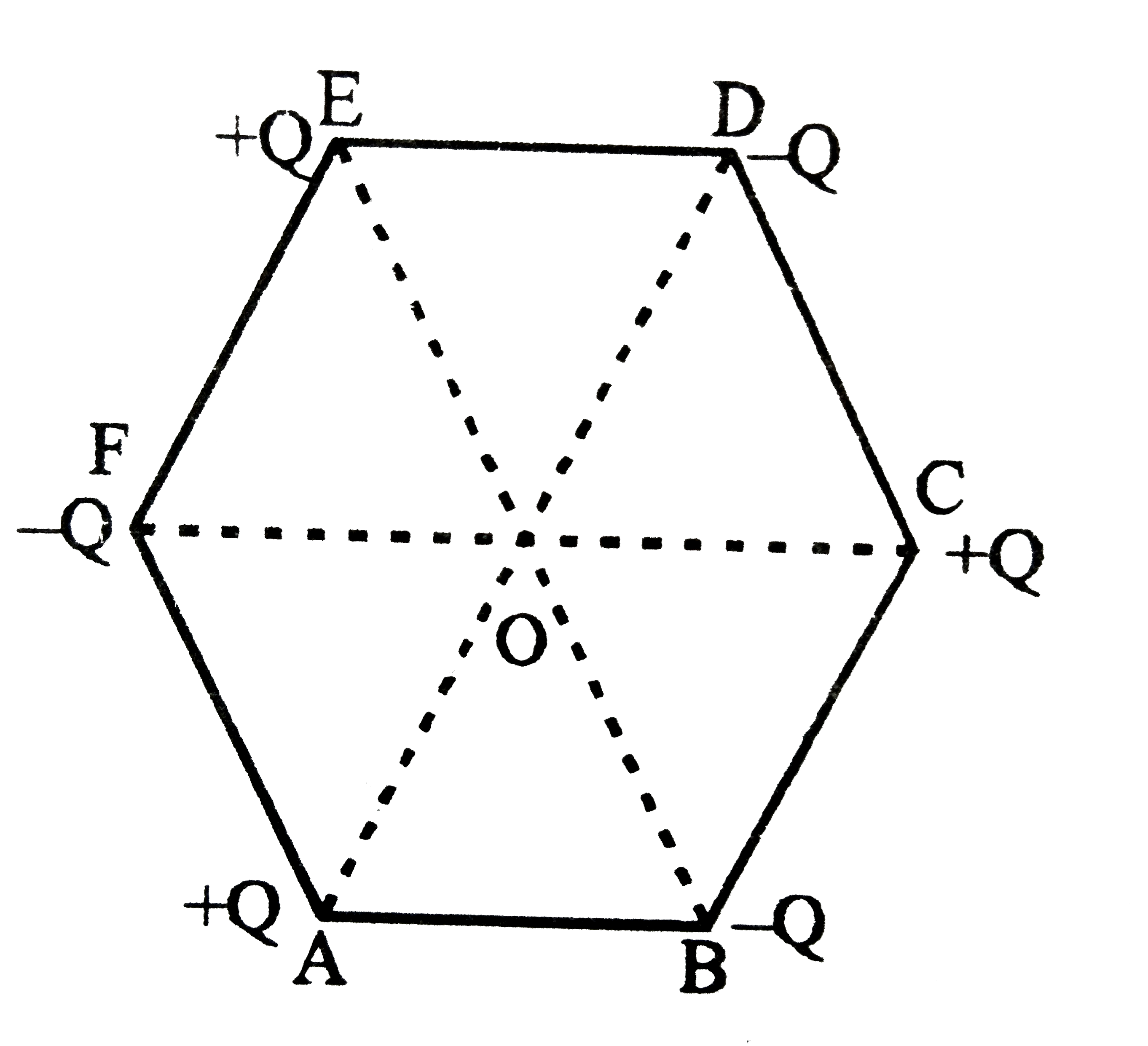
Six point charges are placed at the vertices of a regular hexagon of side a as shown. If E represents electric field and V represents electric potential at O then,
 AE = 0 but V ≠ 0BE ≠ 0 but V = 0CE = 0 and V = 0DE ≠ 0 and V ≠ 0
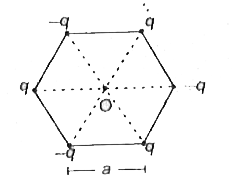
AE = 0 but V ≠ 0BE ≠ 0 but V = 0CE = 0 and V = 0DE ≠ 0 and V ≠ 0Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
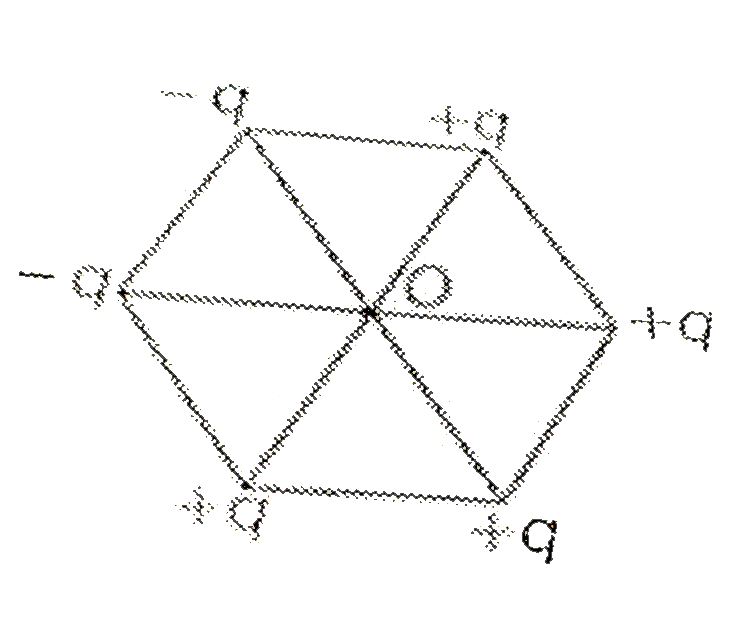
Find the magnitude of electric field at the centre of regular hexagon.Aq4πε0a2BzeroCq2πε0a2Dnone of thesePositive point charges are placed at the vertices of a star shape as shown in the figure. Direction of the electrostatic force on a negative point charge at the centre O of the star is
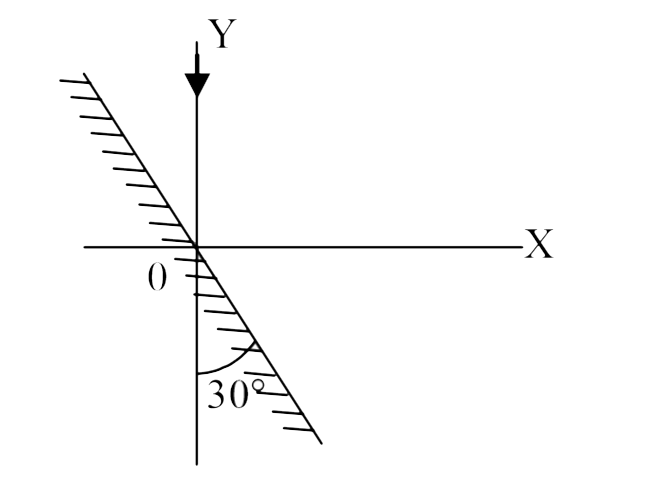 Atowards rightBvertically upCtowards leftDvertically down
Atowards rightBvertically upCtowards leftDvertically down
The point charges are placed on the vertices of regular hexagon of side L as shown. Find the potential energy of the system of charges.
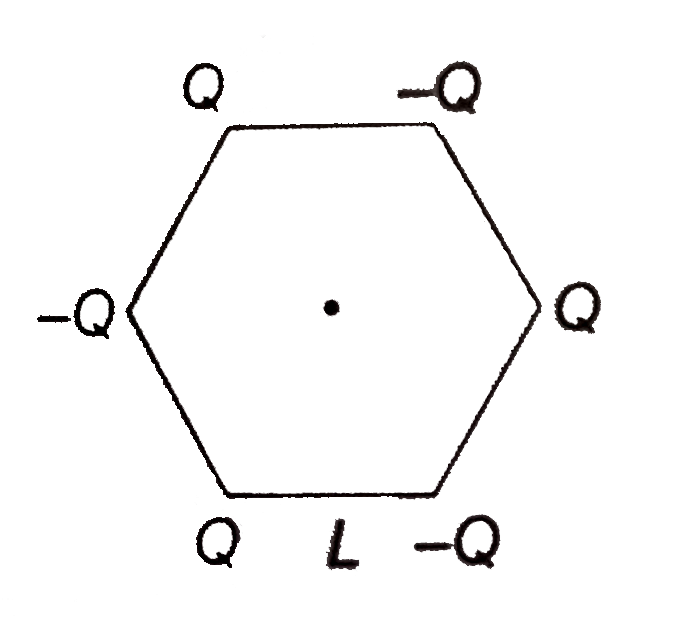
View SolutionSix charges are kept at the vertices of a regular hexagon as shown in the figure. If magnitude of force applied by +Q on +q charge is F, then net electric force on the +Q is nF. Find the value of n.
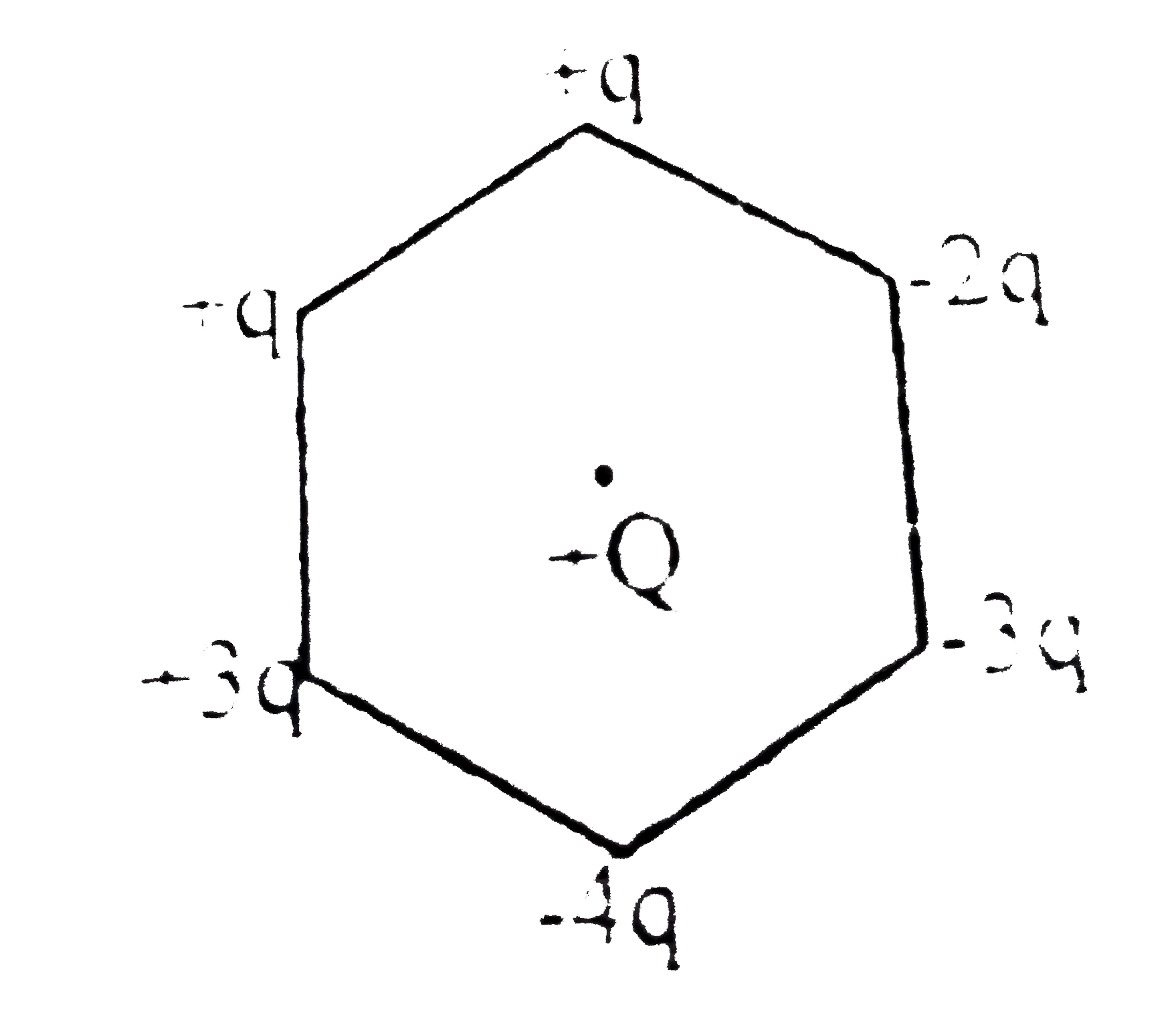
View SolutionSix charges are placed at the corner of a regurlar hexagon as shown . If an electron is placed at its centre O, force on it will be :

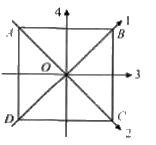
View SolutionThe moment of inertia of a thin square plate ABCD, as shown A in the figure, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of
View SolutionFive point charges each of charge + q are placed on five vertices of a regular of side h as shown in the figure. Then
View Solution