Two aeroplanes are moving towards each other and cross each other. Then the apparent pitch
first decreases and after crossing it increases
first increases and after crossing it decreases
first remains constant and then decreases
continuously increases
The correct Answer is:B
To solve the problem regarding the apparent pitch of two aeroplanes moving towards each other, we can follow these steps:
1. Understanding the Situation:
- Two aeroplanes are moving towards each other. Let's denote the speed of sound in air as v, the speed of the first aeroplane as v1, and the speed of the second aeroplane as v2.
2. Frequency of Sound:
- The frequency of the sound emitted by the source (aeroplane) is denoted as f0.
3. Apparent Frequency Calculation:
- When two sources are moving towards each other, the apparent frequency f′ can be calculated using the Doppler effect formula.
- For the observer moving towards the source, the formula is:
f′=f0(v+vov−vs)
- Here, vo is the speed of the observer (which can be considered as v2 for the second aeroplane) and vs is the speed of the source (which can be considered as v1 for the first aeroplane).
4. Applying the Formula:
- Since both aeroplanes are moving towards each other, we can substitute vo=v2 and vs=v1:
f′=f0(v+v2v−v1)
5. Analyzing the Changes:
- As both aeroplanes approach each other, the numerator (v+v2) increases while the denominator (v−v1) decreases.
- This results in an increase in the apparent frequency f′.
6. Conclusion:
- Therefore, the apparent pitch (or frequency) of the sound will first increase as they approach each other and then will decrease after they cross each other.
- Two aeroplanes are moving towards each other. Let's denote the speed of sound in air as v, the speed of the first aeroplane as v1, and the speed of the second aeroplane as v2.
- The frequency of the sound emitted by the source (aeroplane) is denoted as f0.
- When two sources are moving towards each other, the apparent frequency f′ can be calculated using the Doppler effect formula.
- For the observer moving towards the source, the formula is:
f′=f0(v+vov−vs)
- Here, vo is the speed of the observer (which can be considered as v2 for the second aeroplane) and vs is the speed of the source (which can be considered as v1 for the first aeroplane).
- Since both aeroplanes are moving towards each other, we can substitute vo=v2 and vs=v1:
f′=f0(v+v2v−v1)
- As both aeroplanes approach each other, the numerator (v+v2) increases while the denominator (v−v1) decreases.
- This results in an increase in the apparent frequency f′.
- Therefore, the apparent pitch (or frequency) of the sound will first increase as they approach each other and then will decrease after they cross each other.
Topper's Solved these Questions
Similar Questions
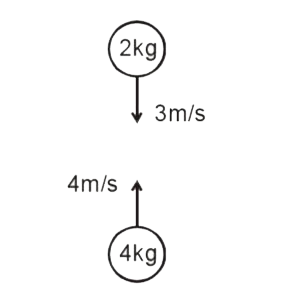
Two balls are moving towards each other on a vertical line collides with each other as shown. Find their velocities just after collision.
View SolutionTwo trains P and Q whose front ends are 539 km apart. They start at the same time towards each other and cross each other after 200 minutes. The ratio of length of these trains is 3 ∶ 2 and their speeds are 90 km/hr and 72 km/hr. Find the difference of the length of these two trains.
View Solution
Knowledge Check
Two trains are moving towards each other and cross each other. The apparent pitch
Afirst decreases and after crossing it increasesBfirst increases and after crossing it decreasesCcontinuously increasesDcontinuously decreaseTwo aeroplanes are moving towards each other. One of them blows a horn the person in the other plane hears the sound. The apparent pitch will
Abecome infiniteBdecreaseCbecome zeroDincreaseTwo aeroplanes A and B are moving towards each other with a speed of 120 m/s. The frequency of the shistle emitted by A is 100 Hz. What is the apparent frequency of the whistle as heard by the captain of plane B?
(Velocity of sound in air = 360 m/s)A500 HzB1500 HzC2000 HzD2500 Hz
A plane mirror and a person are moving towards each other with same velocity v. Then the velocity of the image is
View SolutionTwo boats are traveling towards each other in a stream.
They both can travel at 30 kmph in still water. If they are
300 km apart how long will it take them to cross each other
if the speed of the stream is 5 kmph?
View SolutionWhen an observer moves towards a stationary source, then the apparent pitch will
View SolutionTwo pulse in a stretched string whose centers are initially 8cm apart are moving towards each other as shown in the figure. The speed of each pulse is 2cm/s. After 2seconds, the total energy of the pulse will be
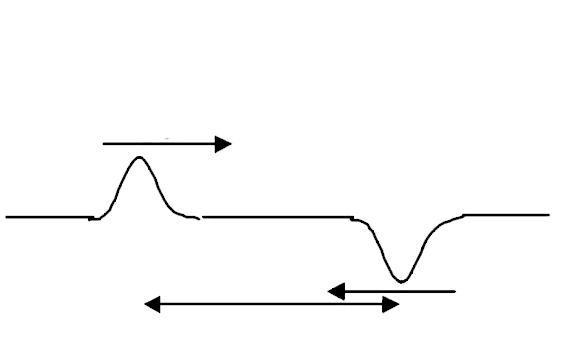
View SolutionTwo pulses in a stretched string whose centres are initially 8 cm apart are moving towards each other as shown in the figure. The speed of each pulse is 2 cm/s. After 2 second, the total energy of the pulses will be

View Solution
