Three particles each of mass m are kept at the vertices of an equilateral triangle of side L . What is the gravitational potential at the centroid of the triangle?
zero
−3√3Gma
−2√3Gma
−√3Gma
The correct Answer is:b
Given AB=BC=AC=a (See figure). The perpendiculars from A, B and C on opposite side meet at the centroid O, which bisect the sides AB, BC and AC. Let r=AO=BO=CO. Centroid alos divides the lines AD, BE and CF in the ratio 2:1, i.e.,
AO=23AD,BO=23BE,CO=23CF
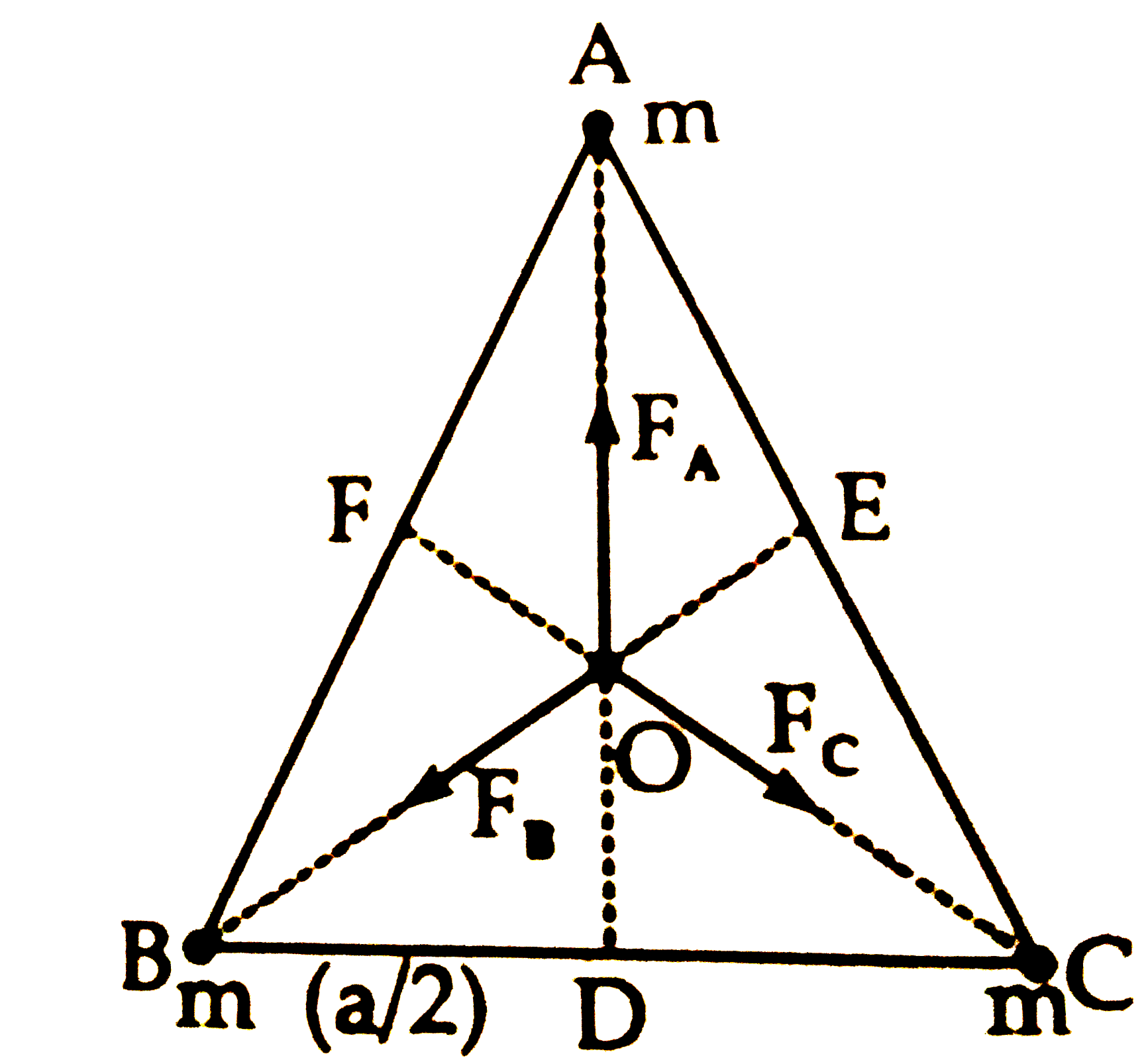
In triangle ABD,
AD=asin60∘=√3a2
Similarly,
BE=CF=√3a2
∴ r=AO=OB=OC=23×√3a2=a√3
V=V1+V2+V3
V=V1+V2+V3
V=−Gmr−Gmr−Gmr
=3Gmr=−3Gma/√3=−3√3Gma
Topper's Solved these Questions
Similar Questions
Three mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View SolutionThree identical point objects each of mass m are placed at the vertices of an equilateral triange of side l. What is the gravitational potential at the centre of the equilateral triangle due to the point masses?
View Solution
Knowledge Check
Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
AzeroB3GML2C9GML2D2GML2Three particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
AzeroB3GML2C9GML2D12GM√3L2Three particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A−3Gm22bB−Gm22bC−3Gm2bD−Gm2b
Three particles, each of mass m are placed at the vertices of an equilateral triangle of side a. What are the gravitation field and gravitational potential at the centroid of the triangle.
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View SolutionIf two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
The gravitational potential at O is
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View Solution
